| 최소신장트리
- Mininum Spanning Tree
- 그래프의 모든 노드를 연결할 때 가중치 합이 최소가 나오는 트리
- 특징 :
(1) 사이클 제외 -- 가중치의 합은 사이클이 포함될 때 최소가 될 수 없다.
(2) N개의 노드에 대한 최소신장트리 간선 수는 늘 N - 1개이다.
| 종류
| |
크루스칼(Kruskal) |
프림(Prim) |
| 핵심 |
- 최소값의 간선 우선 연결
- 사이클 발생 시 다른 간선 선택 |
- 임의의 노드에서 시작
- 연결된 간선 중 낮은 가중치 선택 |
| 언제? |
- 간선 수가 비교적 적을 때 |
- 간선 수가 많을 때 유리 |
| 메모리 |
에지 리스트(or 배열)
유니온 파인드 배열 |
인접 리스트(or 배열)
방문 배열 |
| 속도 |
O(ElogE) |
O(ElogV) - 우선순위 큐 사용 시
*O(v2) - 정렬되지 않은 배열을 사용할 때 |
| 크루스칼 구현
- 구현 순서
| 1 |
에지 리스트(그래프) & 유니온 파인드 배열 초기화 |
| 2 |
에지 리스트를 가중치 기준으로 정렬 |
| 3 |
가중치가 낮은 에지부터 연결하기 반복 |
[1] 에지 리스트(그래프) 정렬 & 유니온 파인드 배열 초기화
- 수업 시간의 경우, 아예 외부에서 입력값으로 미정렬된 간선 배열을 받는 것을 가정으로 했다.
- 이 경우에는 위의 [1][2]를 묶어 간선 배열을 정렬하면 된다.
// 전역변수로 유니온-파인드 배열 지정
static int[] parents;
// data : 간선배열, v : 노드 수, e : 간선 수
public static int kruskal(int[][] data, int v, int e) {
int weightSum = 0; // 전체 가중치
// 1. 그래프 및 유니온 파인드 배열 초기화
// 1-1. 그래프 정렬
Arrays.sort(data);
// 1-2. 유니온 파인트 배열 초기화
parents = new int[v + 1];
for (int i = 1; i < v + 1; i++){
parents[i] = i; // 처음에는 자기 자신
}
return weightSum;
}
[2] 가중치가 낮은 에지부터 연결하기 x 반복
- 가중치가 낮은 에지부터 연결을 하려면 먼저 아래와 같은 메소드가 필요하다.
- 참고로 수업시간에 받은 간선 배열은 무방향 간선들로, 모두 (작은 숫자 노드 -> 큰 숫자 노드)로 연결되어 있었다.
2-1. find(int a) :: int
public static int find(int a){
// 자기 자신과 연결된 경우
if (parents[a] == a){
return a;
}
// 자기 자신과 연결되지 않은 경우
return parents[a] = find(parents[a]);
}
2-2. union(int a, int b) :: void
public static void union(int a, int b){
int aP = parents[a];
int bP = parents[b];
if (aP != bP){ // 여기서는 크기비교x (필요할 경우 추가)
parents[aP] = bP;
}
}
2-3. 최소값 우선으로 간선 연결
public static int kruskal(int[][] data, int v, int e){
// 생략
// 2. 최소값 우선 간선 연결
for (int i = 0; i < e; i++){
// 서로 연결된 적이 없었던 경우
if (find(data[i][0]) != find(data[i][1]){
// 연결
union(data[i][0], data[i][1]);
// 전체 가중치 값 갱신
weightSum += data[i][2];
}
}
}
- 전체 코드
static int[] parents;
public static int kruskal(int[][] data, int v, int e) {
int weightSum = 0;
// 1. 그래프 및 유니온 파인드 배열 초기화
// edge graph
Arrays.sort(data, (x, y) -> x[2] - y[2]);
// union-find
parents = new int[v + 1];
for (int i = 1; i < v + 1; i++) {
parents[i] = i; // 최초에는 자기자신
}
// 2. 최소값 우선으로 간선 연결
for (int i = 0; i < e; i++) {
if (find(data[i][0]) != find(data[i][1])) {
union(data[i][0], data[i][1]);
weightSum += data[i][2];
}
}
return weightSum;
}
public static void union(int a, int b) {
int aP = find(a);
int bP = find(b);
if (aP != bP) {
parents[aP] = bP;
}
}
public static int find(int a) {
if (a == parents[a]) {
return a;
}
return parents[a] = find(parents[a]);
}
| 프림 구현
- 구현 순서
| 1 |
인접 리스트 및 방문 배열 초기화 |
| 2 |
우선 순위 큐를 통해 자동 정렬 |
| 3 |
임의의 노드(ex. 1)를 선택한 후 낮은 가중치의 간선 연결 x 노드 수만큼 반복 |
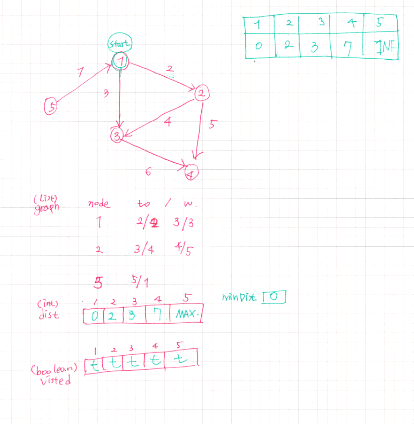
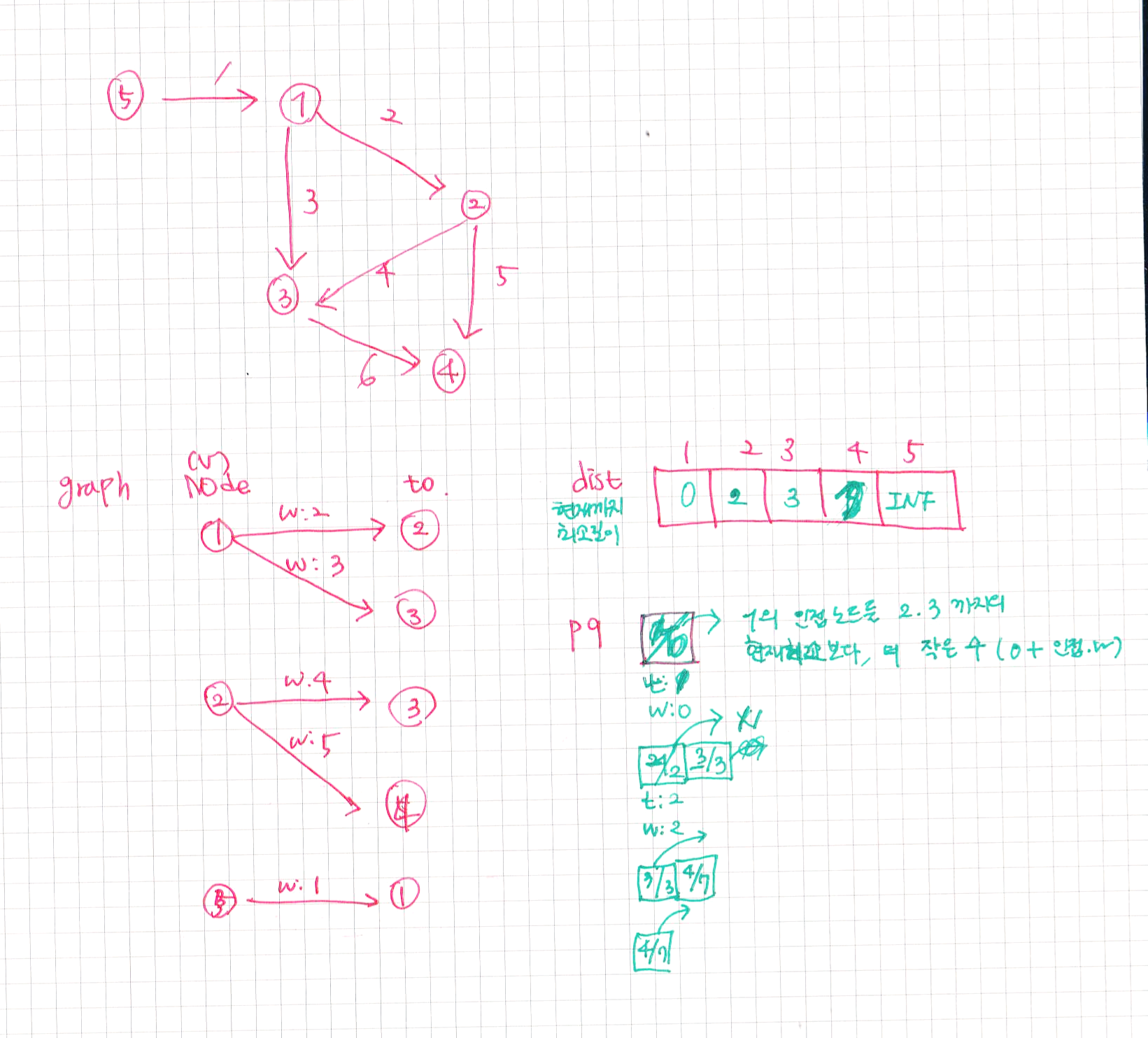
- 원리
입력받은 간선 데이터
int[][] graph =
{{1, 3, 1}, {1, 2, 9}, {1, 6, 8},
{2, 4, 13}, {2, 5, 2}, {2, 6, 7},
{3, 4, 12},
{4, 7, 17}, {5, 6, 5}, {5, 7, 20}};
(1) 방문 배열 : 총 노드의 수(v)만큼 방문배열이 입력된다.
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 |
t |
|
|
|
|
|
|
| 2 |
t |
|
t |
|
|
|
|
| 3 |
t |
|
t |
|
|
t |
|
| 4 |
t |
|
t |
|
t |
t |
|
| 5 |
t |
t |
t |
|
t |
t |
|
| 6 |
t |
t |
t |
t |
t |
t |
|
| 7 |
t |
t |
t |
t |
t |
t |
t |
(2) 우선순위 큐
- 가중치의 크기를 기준으로 오름차순 자동 정렬
- 가장 작은 가중치의 노드를 꺼내, 방문 배열을 체크하고, 전체 가중치(weightSum)를 +하는 형태
* 방문했던 노드는 다시 방문하지 않는다면, 결과적으로는 1-3-6-5-2-4-7 과 같이 노드가 연결될 것
- 타입 : Node (도착노드, 가중치)
| 흐름 |
우선순위 큐 |
| 초기 |
N(1, 0) |
|
|
|
|
| 1 |
N(3, 1) |
N(6, 8) |
N(2, 9) |
|
|
| 2 |
N(6, 8) |
N(2, 9) |
N(4, 12) |
|
|
| 3 |
N(5, 5) |
N(2, 7) |
N(2, 9) |
N(4, 12) |
|
| 4 |
N(2, 5) |
N(6, 5) |
N(2, 7) |
N(2, 9) |
N(4, 12) |
| 5 |
N(6, 5) |
N(2, 7) |
N(2, 9) |
N(4, 12) |
N(4, 13) |
| 6 |
N(4, 13) |
N(7, 17) |
|
|
|
- 구현
[1] 인접 리스트 및 방문 배열 초기화
static class Node{
int to;
int weight;
Node(int to, int weight;){
this.to = to;
this.weight = weight;
}
}
public static int prim(int[][] data, int v, int e){
// 인접리스트
ArrayList<ArrayList<Node>> adjList = new ArrayList();
for (int i = 0; i < v + 1; i++){
adjList.add(new ArrayList());
}
for (int i = 0; i < e; i++){
// 양방향으로 저장
adjList.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
adjList.get(data[i][1]).add(new Node(data[i][0], data[i][2]));
}
// 방문 배열
boolean[] visited = new boolean[v + 1];
}
[2] 우선 순위 큐를 통해 자동 정렬
public static int prim(int[][] data, int v, int e){
// 생략
// 우선순위 큐
PriorityQueue<Node> pq = new PriorityQueue((x, y) -> x.weight - y.weight);
}
[3] 임의의 노드(ex. 1)를 선택한 후 낮은 가중치의 간선 연결 x 노드 수만큼 반복
public static int prim(int[][] data, int v, int e){
// 생략
// 우선순위 큐
PriorityQueue<Node> pq = new PriorityQueue((x, y) -> x.weight - y.weight);
pq.add(new Node(1, 0)); // 임의의 노드를 시작점으로 지정
int cnt = 0; // 노드만큼만 반복
while (!pq.isEmpty()){
Node cur = pq.poll();
cnt++;
// 방문 여부확인
if (visited[cur.to]){
continue;
}
visited[cur.to] = true; // 방문 체크
weightSum += cur.weight; // 전체 가중치 갱신
// 반복 수 확인(마지막 뽑는 노드)
if (cnt == v) {
break;
}
// 인접한 정점을 작은 가중치 순으로 offer
for (int i = 0; adjList.get(cur.to).size(); i++){
Node adjNode = adjList.get(cur.to).get(i);
if (visited[adjNode.to]) {
continue;
}
pq.offer(adjNode);
}
}
return weightSum;
}
- 전체 코드
static class Node {
int to;
int weight;
public Node(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
public static int prim(int[][] data, int v, int e) {
int weightSum = 0;
ArrayList<ArrayList<Node>> adjList = new ArrayList();
for (int i = 0; i < v + 1; i++) {
adjList.add(new ArrayList<>());
}
for (int i = 0; i < e; i++) {
// 양방향으로 연결
adjList.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
adjList.get(data[i][1]).add(new Node(data[i][0], data[i][2]));
}
boolean[] visited = new boolean[v + 1];
PriorityQueue<Node> pq = new PriorityQueue<>((x, y) -> x.weight - y.weight);
pq.add(new Node(1, 0));
int cnt = 0;
while (!pq.isEmpty()) {
Node cur = pq.poll();
cnt++;
if (visited[cur.to]) {
continue;
}
visited[cur.to] = true;
weightSum += cur.weight;
if (cnt == v) {
return weightSum;
}
// 인접한 정점을 작은 가중치 순으로 offer
for (int i = 0; i < adjList.get(cur.to).size(); i++) {
Node adjNode = adjList.get(cur.to).get(i);
if (visited[adjNode.to]) {
continue;
}
pq.offer(adjNode);
}
}
return weightSum;
}
[ 참고 및 출처 ]
- 부트캠트 수업 내용 정리
- [Do it! 알고리즘 코딩 테스트 자바 편]