| 분할정복이란?
- 폰노이만 구조를 만든 그 폰노이만에 의해 소개된 알고리즘
- 간략하게 말하면, 큰 문제를 작은 단위로 쪼갠 후 다시 조합하여 문제를 해결하는 방법을 말한다.
분할: 문제를 더이상 분할할 수 없을 때까지 동일한 유형의 여러 하위 문제로 나눈다.
정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다
*출처 : 나무위키
| 분할정복 과정
1. 문제를 하나 이상의 작은 단위로 분할
2. 작은 단위에서 부분적인 해결
3. 부분들의 해결을 조합해 전체 문제의 해답을 찾는다.
function F(x):
if F(x)가 간단 then:
return F(x)를 계산한 값
else:
x 를 x1, x2로 분할
F(x1)과 F(x2)를 호출
return F(x1), F(x2)로 F(x)를 구한 값
* 출처 : 나무위키
| 장단점
| 장점 | 어려운 문제를 해결할 수 있다 병렬적으로 문제를 해결하는데에 이점이 있다. |
| 단점 | 메모리 사용량이 높다(재귀 호출을 통한 오버헤드 발생) |
| 예시
분할정복의 예시로 자주 거론되는 것으로 아래 네 가지가 있다.
이 중에서 내 단계에서 언급하기 쉬워 보이는 1~3의 알고리즘만 적어보려고 한다.
1. 합병 정렬
2. 퀵소트
3. 카라추바 알고리즘
4. 고속 푸리에 변환
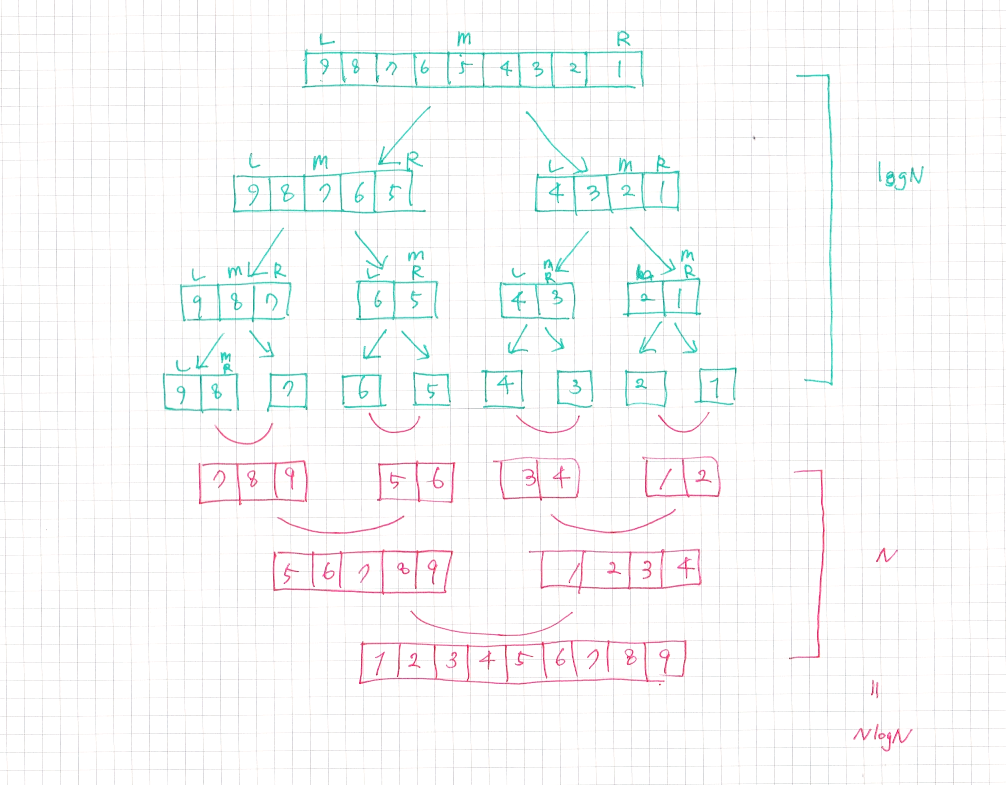
1. 합병정렬
- 분할정복과 투포인터의 특성을 사용해서 만들어진 정렬이라 볼 수 있을 것 같다.
- 1) 먼저 배열의 범위를 투 포인터를 통해 분할하여 지정한 후에,
- 2) 작은 범위에서 데이터를 비교하여 정렬을 하고
- 3) 작은 범위를 조합하여 전체 정렬을 이루는 과정
void mergeSort(int[] arr, int[] tmp, int left, int right){
if (left < right) {
int mid = (left + right) / 2;
// mid를 기준으로 배열을 분할한다.
mergeSort(arr, tmp, left, mid);
mergeSort(arr, tmp, mid + 1, right);
// mid를 기준으로 배열을 조합한다.
merge(arr, tmp, left, right, mid);
}
}
void merge(int[] arr, int[] tmp, int left, int right, int mid){
// mid를 기준으로 좌/우 포인터,
// index포인터를 준비하고
int l = left;
int r = mid + 1;
int idx = left;
// 좌/우 포인터를 비교하여 tmp에 오름차순으로 저장
// 적어도 두 포인터 중 하나가 범위 내에 있을 때에
while (l <= mid || r <= right){
// 조건1 : 모든 포인터가 범위내에 있다면
if (l <= mid && r <= right){
// 두 포인터의 데이터를 비교해서
// 더 작은 데이터를 tmp에 넣고, 포인터를 하나 증가한다.
if (arr[l] <= arr[r]){
tmp[idx++] = arr[l++];
} else {
tmp[idx++] = arr[r++];
}
}
// 조건2 : left포인터만 범위내에 있다면
else if (l <= mid && r > right){
tmp[idx++] = arr[l++];
}
// 조건3 : right포인터만 범위내에 있다면
else {
tmp[idx++] = arr[r++];
}
}
// tmp의 데이터를 arr에 옮긴다.
for (int i = left; i <= right; i++){
arr[i] = tmp[i];
}
}
2. 퀵소트
- 피봇이라는 기준값을 토대로 투포인터와 분할정복을 활용한 정렬 알고리즘이다.
- 1) 먼저 피봇값이라는 기준값을 지정하고 반정렬
- 2) 피봇값을 기준으로 배열을 분할
- 3) 분할된 배열을 부분적으로 정렬

void quickSort(int[] arr, int left, int right){
// 탈출문
if (left >= right) {
return;
}
// 피봇값을 지정
int pivot = partition(arr, left, right);
// 피봇값을 기준으로 배열을 분할
quickSort(arr, left, pivot - 1);
quickSort(arr, pivot + 1, right);
}
void int partition(int[] arr, int left, int right){
// 투 포인터와 피봇값 지정
int l = left;
int r = right;
int pivot = arr[left];
// 피봇값을 기준으로 양 끝 포인터를 올리거나 내려준다
while(l < r) {
while (arr[r] > pivot && l < r) {
r--;
}
while (arr[l] <= pivot && l < r) {
l++;
}
swap(arr, l, r);
}
// 기존 피봇값 위치 데이터와 피봇값을 교환
swap(arr, left, l);
return l;
}
3. 카라추바 알고리즘
- 카라추바라는 사람이 1960년에 만든 분할정복 알고리즘으로,
- 초등학교 곱셈 공식에서 배웠던 각 자릿수를 곱하는 방식을 응용해 만든 알고리즘이다.
- 알고리즘 구현의 단계는 아래와 같다.
1. z0 = a * c
2. z1 = b * d
3. z2 = (a + b)(c + d)
4. z3 = z0 - ac - bd
5. (z0 * 10^n) + (z3 * 10^(n/2)) + z1
- 아래 코드 외에 아예 ArrayList를 사용해서 각 자릿수를 저장하는 방식 또한 있는데,
굉장히 복잡하기 때문에 관련된 코드는 검색을 통해 복사하여 사용하는 편이 좋을 것 같다.
** 자바에는 BigInteger라는 큰 수를 다루는 객체가 따로 있다.
(큰 수의 곱셈은 이 객체의 multiply() 메소드를 쓰는 것이 코드를 가독성 있게 짜기에는 더 좋아 보인다.)
public static long karatsuba(long x, long y) {
// 범위가 작은 경우
if (x <= 50 && y <= 50) {
return x * y;
}
// a와 b의 자릿수
int numXLen = (int)Math.log10(x);
int numYLen = (int)Math.log10(y);
// a와 b의 자릿수 중에 더 큰 자릿수를 선택
int maxLen = Math.max(numXLen, numYLen); // ex 1234 -> 4
// 분할한 자릿수
Integer halfMaxLen = (maxLen / 2) + (maxLen % 2); // ex 1234 -> 2
// Multiplier : 곱할 10^n
long halfMaxLenTen = (long)Math.pow(10, halfMaxLen); // ex 1234 -> 10^2
// 분할한 수들을 구한다.
long a = x / halfMaxLenTen;
long b = x % halfMaxLenTen;
long c = y / halfMaxLenTen;
long d = y % halfMaxLenTen;
// 4단계에 따라 각 수들을 곱하고 더한다.
// 1. a * c
// 2. b * d
// 3. (a+b)(c+d)
// 4. (3)에서 (1), (2)를 뺀다
// 5. (1) x halfMaxLen + (2) + (4) x (halfMaxLen / 2)
long z0 = karatsuba(a, c);
long z1 = karatsuba(b, d);
long z2 = karatsuba(a + b, c + d);
long z3 = z2 - z1 - z0;
long res = (z0 * (long)Math.pow(10, halfMaxLen * 2)) + (z3 * (long)Math.pow(10, halfMaxLen)) + z1;
return res;
}
| 백준 문제
- 백준의 분할 정복에 대한 문제는 사실상 재귀 문제와 별반 다를게 없었다.
- 그만큼 재귀와 분할정복이 서로 땔래야 땔 수 없는 관계라는 것을 의미하는 듯 하다.
https://www.acmicpc.net/workbook/view/798
문제집: 분할정복 (cokcjswo)
www.acmicpc.net
[ 출처 및 참조 ]
- 부트 캠프 강의를 들은 후 정리한 내용입니다.
- [Do it! 알고리즘 코딩 테스트 - 자바 편]
- 나무위키, https://namu.wiki/w/%EB%B6%84%ED%95%A0%20%EC%A0%95%EB%B3%B5%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://www.geeksforgeeks.org/java-program-to-implement-the-karatsuba-multiplication-algorithm/
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] DP (동적 계획법) (0) | 2022.08.26 |
|---|---|
| 모듈러 산술 (0) | 2022.08.25 |
| [알고리즘] 그리디 (0) | 2022.08.25 |
| [알고리즘] 탐색 - DFS, BFS, 이진 탐색 (0) | 2022.08.25 |
| HashSet<int[]>와 Hashset<ArrayList<Integer>> (0) | 2022.08.17 |