심플하고 차분하게

시작하기 전에 - 가상화 기술의 종류 돌아보기

 
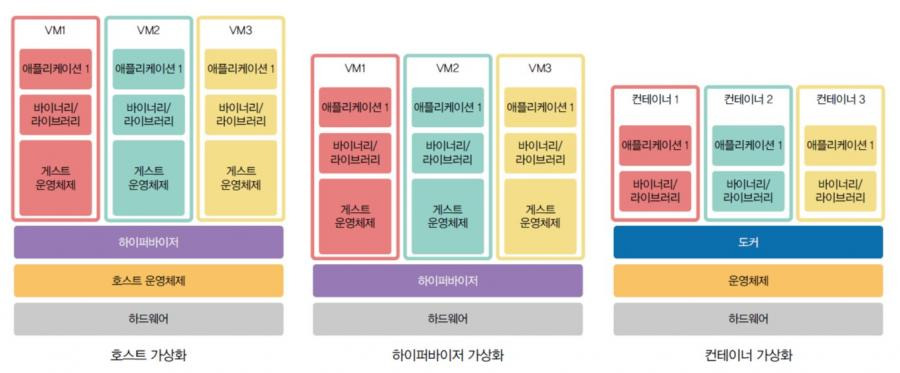
가상화 기술은 크게 세 가지로 나뉜다. 1) 호스트 가상화, 2) 하이퍼바이저 가상화, 3) 컨테이너 가상화.
호스트 가상화의 경우, 호스트 OS에 설치 프로그램을 받아 실행하는 것으로 게스트 OS를 쓰는 방식을 말한다.
하이퍼 바이저는, Windows에 딸려있는 Hyper-V 같이 하드웨어에 붙어 있는 가상화 기술을 말한다. 
컨테이너는, Docker 같이 각각의 컨테이너로 격리된 공간을 나누고, 호스트 OS의 자원을 공유할 수 있게 한 기술을 말한다.  
이번에 설치하는 Oracle Virtualbox는 이 중에서도 호스트 가상화 기술을 사용한 것이다.
 

준비 

Oracle Virtualbox 및 Mac OS 이미지를 다운로드한다.
* 가급적 Mac OS 버전을 13 이상으로 까는 걸 추천한다. Redcat 같은 앱은 버전 13 이상이어야 가능..
 
[1] Oracle Virtualbox 프로그램 설치 [바로가기]
[2] Oracle Virtualbox 프로그램 확장팩 설치 [바로가기]
[3] Mac OS 버전 이미지 다운로드
[4] 현재 내 컴퓨터가 가상화 기술을 허용하고 있는지 확인 - 부팅할 때 ESC를 눌러서 세팅화면으로 넘어가서 확인하기 
 
 

가상머신 생성하기

 
[1] [새로만들기] 를 눌러 가상 머신을 만든다.

 
[2] 가상머신의 이름을 작성하고 종류는 Mac OS X, 버전은 Mac OS X (64-bit)
 
* 버전의 경우, 사용하려는 Mac OS 이미지 버전과 맞는 것을 고르는 게 좋다. 그렇지 않으면 제대로 설치가 안 된다. 
* 만약, 처음 [새로 만들기]를 누르는 게 아니라면, ISO 이미지를 여기서 추가해줘도 좋다. 

 
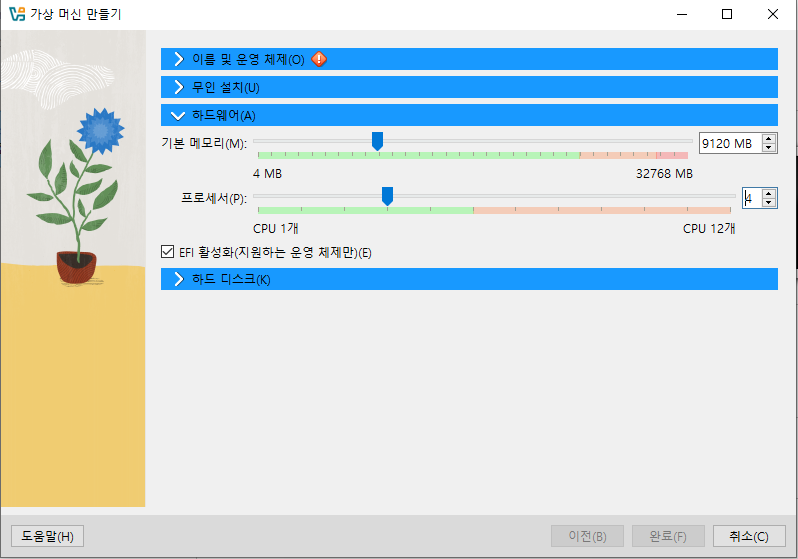
[3] 하드웨어의 기본 메모리를 9000 MB 이상, 프로세서를 2개 이상으로 설정한다.
 
* 실제로 해보면 프로세서 2개도 느렸다. 나는 가상머신 쓸 때 호스트OS로 작업을 안 할 거라, 그냥 4개로 넣어줬다. 

 
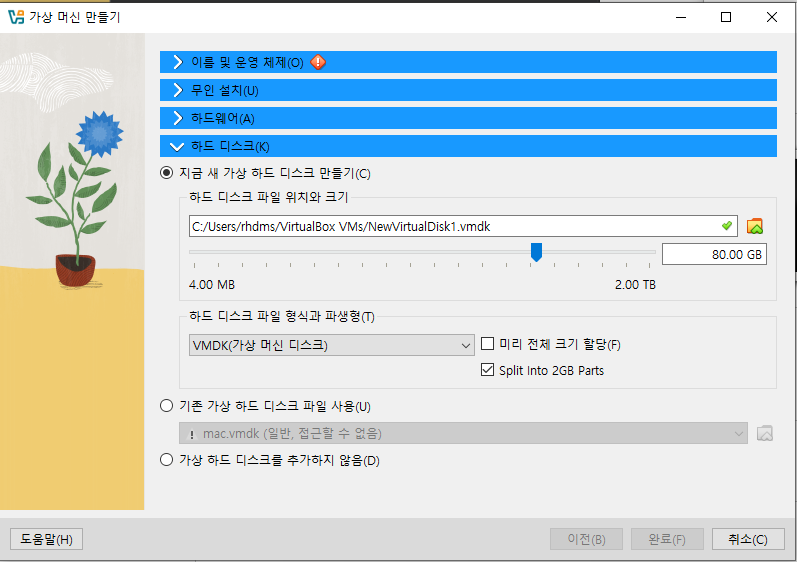
[4] 새 하드디스크를 만들어 준다. 파일 형식은 VMDK로 하고 Split into 2GB Parts에 체크를 해준다.

설정 세팅

 
[1] [시스템] - [마더보드]의 설정을 체크한다.
- 플로피 체크해제
- 칩셋 : ICH9
- 포인팅 장치 : USB 태블릿
- EFI 활성화

 
[2] [시스템]-[프로세서] 에서 PAE/NX 가 활성화 되어있는지 확인

 
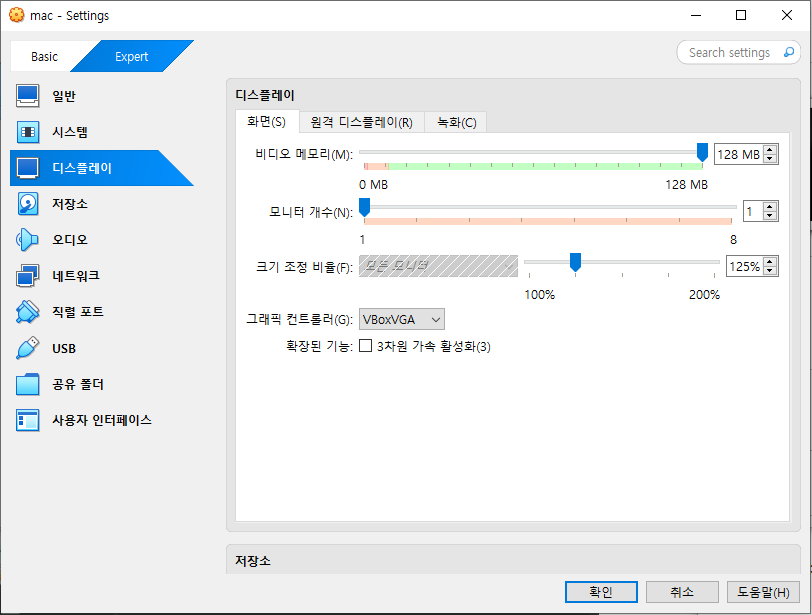
[3] [디스플레이]-[화면] 에서 "비디오 메모리"를 128MB로 수정, 그래픽 컨트롤러도 VBoxVGA를 사용한다.

 
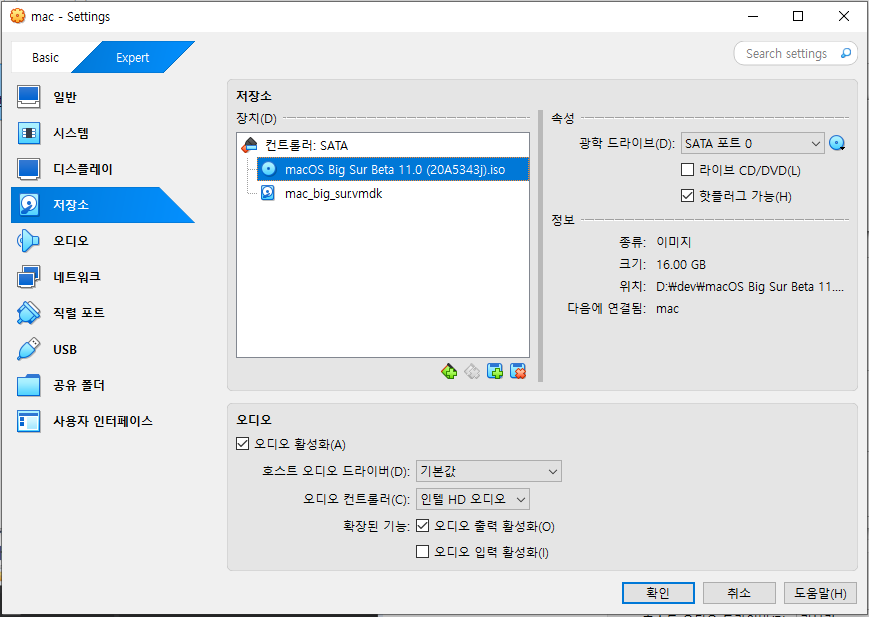
[4] [저장소]에서 컨트롤러 SATA의 "호스트 I/O 캐시 사용"에 체크 

 
[5] 아래와 같이 ISO 가 먼저 올 수 있게 SATA 포트를 0으로 설정해 준다.

CLI에서 스크립트 실행하기

Virtualbox에서 MacOS를 가상화하기 위해서는 CPU ID, DMI 정보, SMC 설정, CPU 프로필 설정을 해야한다. 
 
[1] Windows에서 CMD창을 관리자 권한으로 실행하고, 아래의 코드를 입력해 설정을 시도한다.

cd "C:\Program Files\Oracle\VirtualBox"

VBoxManage.exe modifyvm "macOS" --cpuidset 00000001 000106e5 00100800 0098e3fd bfebfbff
VBoxManage setextradata "macOS" "VBoxInternal/Devices/efi/0/Config/DmiSystemProduct" "imacOS19,1"
VBoxManage setextradata "macOS" "VBoxInternal/Devices/efi/0/Config/DmiSystemVersion" "1.0"
VBoxManage setextradata "macOS" "VBoxInternal/Devices/efi/0/Config/DmiBoardProduct" "macOS-AA95B1DDAB278B95"
VBoxManage setextradata "macOS" "VBoxInternal/Devices/smc/0/Config/DeviceKey" "ourhardworkbythesewordsguardedpleasedontsteal(c)AppleComputerInc"
VBoxManage setextradata "macOS" "VBoxInternal/Devices/smc/0/Config/GetKeyFromRealSMC" 1

 
[2] 만약, 부팅 중에 "bdsdxe failed to load boot0001 uefi vbox cd-rom vb1-1a2b3c4d" 에러가 나타난다면 아래를 추가적으로 입력한다. 미리 에러를 막고 싶다면 그냥 [1]에서 같이 입력하는 방법 추천.

VBoxManage.exe modifyvm "macOS" --cpu-profile "Intel Core i7-6700K"

시작하기

Apple 화면이 뜨면 이제 설치를 해주면 된다. 
 
[1] [시작하기]를 눌러서 실행한다. 

 
Apple 화면이 잘 뜬다면 당신은 이제 80% 성공.

 
 
[2] Mac OS 설치 전에, [유틸리티] - [디스크 유틸리티]에서 [보기] 버튼을 클릭, "모든 장치 보기" 또는 "Show All Devices" 선택
 

 
[3] 왼쪽 사이드 바에서 VBOX HARDDISK Media를 선택 (최상위 디스크 선택), 상단의 "지우기" 버튼 클릭
 
- 이름: Macintosh HD (원하는 이름)
- 포맷: APFS
- 구성: GUID 파티션 맵
- "지우기" 클릭
 

 
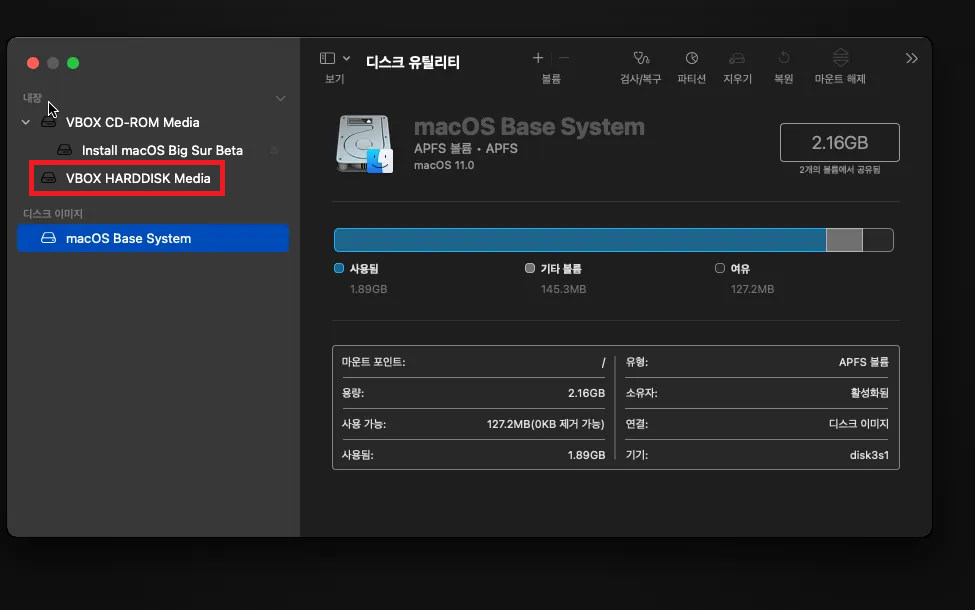
[4] 아래와 같이 내가 설치하고자 하는 디스크 상세 정보가 잘 나오면 됨

 
[5] 다시 앞으로 돌아가서 Mac OS 설치를 시작한다. 

Docker 강의를 듣는 중에 리눅스 OS 사용이 필요해서 WSL을 사용하기로 했다.  

WSL 이란?

Windows Subsystem for Linux의 줄임말로, 윈도우에서 리눅스를 사용할 수 있게 해주는 서브시스템을 의미한다. 

기존 WSL을 사용하면 윈도우 환경에서도 powershell 등을 통해 linux 명령어를 사용할 수 있게 해주었다. 

WSL2에서는 업데이트된 형태로 하이퍼바이저를 통해 Windows 뿐만 아니라, Linux 또한 사용할 수 있도록 해준다.

* Hypervisor : 다수의 VM을 사용할 수 있도록 연결해주는 소프트웨어  

윈도우에서 WSL를 사용하는 명령어

* 윈도우 10 이상에서만 설치 가능 

wsl --install

powershell 또는 cmd 를 관리자 권한으로 열고 위의 명령어를 친 뒤, 재부팅을 해주면 된다.

설치를 했는데 오류가 나는 경우 

wsl/callmsi/e_abort

만약에 위와 같은 오류가 나타난다면, 

윈도우 + R 을 누르고 regedit 를 입력한 뒤, 아래와 같이 WslService를 찾아 삭제 후 재부팅 후 재설치를 하면 된다.

1. Navigate to Computer\HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Services
2. Look for "WslService" -> Right click on folder icon -> Delete
3. Restart PC

WSL 실행하기 

윈도우 > WSL 를 검색하면 WSL를 실행할 수 있다. 

참고  

https://hirlawldo.tistory.com/137

https://dongle94.github.io/windows/windows-wsl-install/

https://github.com/microsoft/WSL/issues/10764

|  관련 강의 영상

https://www.youtube.com/watch?v=UcjK_k5PLHI 

- KMP나 Robin-Karp를 사용하면 O(n)의 시간복잡도로 문자열에서 패턴 문자열을 찾을 수 있다.

- KMP는 어려워서 일단 Robin-karp 부분만 찾아서 적용해보았다.

|  Robin-Karp 알고리즘 사용해보기

https://joomn11.tistory.com/111?category=900637 

public static int robinKarp(String parent, String pattern, int parentSize, int patternSize){

    int parentHash = 0, patternHash = 0, power = 1;
    int result = 0;

    // 슬라이딩 윈도우 방식으로 하나씩 증가
    for (int i = 0; i <= parentSize - patternSize; i++) {
        // 처음에는, 패턴 문자열 길이만큼 해시값을 구한다.
        if (i == 0) {
            for (int j = 0; j < patternSize; j++) {
                parentHash += parent.charAt(j) * power;
                patternHash += pattern.charAt(j) * power;
            }

            if (i < patternSize - 1) {
                power *= 2;
            }
        } 
        // 처음이 아닌 경우, 가장 앞의 문자를 빼고, 새로운 문자를 추가한다.
        else {
            parentHash = (parentHash - parent.charAt(i - 1) * power) * 2
                    + parent.charAt(i + patternSize - 1);
        }

        // 윈도우 위치에서 부모와 패턴이 일치하는 경우
        if (parentHash == patternHash) {
            result++;
        }
    }

    return result;
}

|  알고리즘 속도 구하는 방법

- 아래와 같은 방법으로 알고리즘 속도를 구할 수 있다.

- 예전에 알고 있던 방법이었는데, 금방 잊어버렸기에 생각날 때 노트해두었다.

Long start = System.currentTimeMillis();

// 알고리즘 돌리고

Long end = System.currentTimeMillis();

System.out.prinln(end - start + " ms");

|  소프트웨어 공학의 필요성

- 소프트웨어 공학이란? 시스템 초기부터 오픈 후 유지/보수까지의 소프트웨어 개발과 관련된 모든 측면을 의미

- 왜 필요한가?

  (1) 비용의 문제 (개발 60% + 테스트 40%) : 계획 없는 개발은 추가 비용을 발생시킨다.

  (2) 시스템 복잡도 향상 : 점차 복잡해지는 시스템 속에서 방향성을 잡는 것이 필요해졌다.

- 소프트웨어의 종류

- 좋은 소프트웨어란? 고객에게 필요한 기능과 성능을 제공하는 소프트웨어

  > "높은 다양성과, 믿을 수 있는 소프트웨어"

  > 좋은 소프트웨어가 꼭 가져야하는 특성 : 유지가능성, 신뢰성과 보안, 효율성, 접근가능성(쉽고 단순해야)

|  소프트웨어 프로세스 정형화

1. 전통적인 방식 

- 고객/사용자(Client)/플젝 관리자(PM)/개발자

- SI의 방식과 비슷하다.

- 요구사항 > 요구명세 & 요구분석 > 설계 > 구현 > 테스트 > 납품/유지보수

1-1. 고전적인 개발 방법론

	폭포수 모델	프로토타입 모델	나선형 모델
내용	순차적인 단계	간단한 프로토타입을 만든 후 수정	작은 단위의 task로 점진적 개발
장점	사전 설계가 세부적일 때 유용	폭포수 보다 요구사항 도출 용이	프로토타입 보다 요구사항 파악 쉬움 위험을 최소화할 수 있음 대규모 시스템에 유리
단점	변화에 유동적이지 않음 일정 산출의 어려움	프로토타입을 완제품으로 오해 프로토타입 제작의 비효율성	개발 시간이 오래 소요 시스템이 복잡해 관리가 어려움
img			* 출처 : 나무위키

* 이미지 출처 : https://m.blog.naver.com/PostView.nhn?isHttpsRedirect=true&blogId=seilius&logNo=130185596031 

[ 완벽한 기획이 실제로 가능할까 (더보기) ]

- 고객의 요구사항이 코딩 테스트 문제처럼 세부적일 거란 기대는 하지 않는 게 좋다.

- 처음부터 개발자를 만족시킬 수 있는 기획이 있을까? 그럼 처음부터 고객을 만족시킬 수 있는 개발물은?

2. 오늘날의 개발 방식

- 최신 서비스 특성 : Mobile First, 웹 + 모바일의 서비스 개발, 클라우드 컴퓨팅 기반, 개인정보 보호 강화

- 최신 서비스 개발 Trend :  빠르게 micro 단위로 순차적인 개발을 한다.

   > 새로운 기술, Micro Features

   > 고객 경험을 모니터링 - micro단위로 AB테스트, 고객 로그를 활용

2-1. 최신 소프트웨어 업계 개발방식

Agile이란?

개발과 함께 즉시 피드백을 받아서 유동적으로 개발하는 방법

* 출처 : 나무위키

(1) Agile 선언문

(2) Scrum 프로세스

* Scrum이란? 순차적이고 점진적인 에자일 방식의 개발 과정

1️⃣ Scrum 팀 구성 : 일반적으로 10명 안밖으로 구성된다.

2️⃣ Sprint 계획(1달, 2주) & 진행 

- Sprint : Epic(Story) - Tickets(Backlog) - Priorization - Dev Estimation - Test - Release

- Product Backlog 예시 이미지

3️⃣ Daily Scrum으로 진척사항/변동사항을 확인 후 공유

4️⃣ Sprint 끝나면 진행한 것 리뷰/반성

DevOps란?

- 소프트웨어의 개발(Development)과 운영(Operations)의 합성어로 최근에 새롭게 나타난 조직명이다.

- 역할 : Release System의 자동화, 코드 리뷰 및 테스트 자동화, 서비스 모니터링, 이슈 발생 시 커뮤니케이션 시스템

스타트업과 린 스타트업

- [린 스타트업], Eric Ries 

" 승리할 수 있는 유일한 방법은 다른 누구보다 빨리 배우는 것이다 "

- 스타트업이란? 극심한 불확실성 속에서 신규 제품이나 서비스를 만들고자 하는 조직

|  정리

[ 참조 및 출처 ]

부트캠프 강의를 들은 후 기타 자료와 함께 정리한 내용입니다.

[Software Engineering] 소프트웨어 공학이란?, 소프트웨어 공학의 필요성, 좋은 소프트웨어의 특성

https://velog.io/@katanazero86/%EC%95%A0%EC%9E%90%EC%9D%BCagile%EC%9D%B4%EB%9E%80-%EB%AC%B4%EC%97%87%EC%9D%B8%EA%B0%80

TDD란? https://gmlwjd9405.github.io/2018/06/03/agile-tdd.html

|  최소신장트리

- Mininum Spanning Tree

- 그래프의 모든 노드를 연결할 때 가중치 합이 최소가 나오는 트리

- 특징 : 

(1) 사이클 제외 -- 가중치의 합은 사이클이 포함될 때 최소가 될 수 없다. 

(2) N개의 노드에 대한 최소신장트리 간선 수는 늘 N - 1개이다.

|  종류

|  크루스칼 구현

- 구현 순서

[1] 에지 리스트(그래프) 정렬 & 유니온 파인드 배열 초기화

- 수업 시간의 경우, 아예 외부에서 입력값으로 미정렬된 간선 배열을 받는 것을 가정으로 했다.

- 이 경우에는 위의 [1][2]를 묶어 간선 배열을 정렬하면 된다.

// 전역변수로 유니온-파인드 배열 지정
static int[] parents;

// data : 간선배열, v : 노드 수, e : 간선 수
public static int kruskal(int[][] data, int v, int e) {
    int weightSum = 0; // 전체 가중치
    
    // 1. 그래프 및 유니온 파인드 배열 초기화
    // 1-1. 그래프 정렬
    Arrays.sort(data);
    
    // 1-2. 유니온 파인트 배열 초기화
    parents = new int[v + 1];
    
    for (int i = 1; i < v + 1; i++){
    	parents[i] = i; // 처음에는 자기 자신
    }
    
    return weightSum;
}

[2] 가중치가 낮은 에지부터 연결하기 x 반복

- 가중치가 낮은 에지부터 연결을 하려면 먼저 아래와 같은 메소드가 필요하다.

- 참고로 수업시간에 받은 간선 배열은 무방향 간선들로, 모두 (작은 숫자 노드 -> 큰 숫자 노드)로 연결되어 있었다.

2-1. find(int a) :: int 

public static int find(int a){
	// 자기 자신과 연결된 경우
	if (parents[a] == a){
    	return a;
    }
    // 자기 자신과 연결되지 않은 경우
    return parents[a] = find(parents[a]);
}

2-2. union(int a, int b) :: void

public static void union(int a, int b){
    int aP = parents[a];
    int bP = parents[b];
    
    if (aP != bP){ // 여기서는 크기비교x (필요할 경우 추가)
    	parents[aP] = bP;
    }
}

2-3. 최소값 우선으로 간선 연결

public static int kruskal(int[][] data, int v, int e){
    // 생략
    
    // 2. 최소값 우선 간선 연결
    for (int i = 0; i < e; i++){
    	// 서로 연결된 적이 없었던 경우
        if (find(data[i][0]) != find(data[i][1]){
        	// 연결
            union(data[i][0], data[i][1]);
            // 전체 가중치 값 갱신
            weightSum += data[i][2];
        }
    }
}

- 전체 코드

static int[] parents;
public static int kruskal(int[][] data, int v, int e) {
    int weightSum = 0;

    // 1. 그래프 및 유니온 파인드 배열 초기화
    // edge graph
    Arrays.sort(data, (x, y) -> x[2] - y[2]);

    // union-find
    parents = new int[v + 1];
    for (int i = 1; i < v + 1; i++) {
        parents[i] = i; // 최초에는 자기자신
    }

    // 2. 최소값 우선으로 간선 연결
    for (int i = 0; i < e; i++) {
        if (find(data[i][0]) != find(data[i][1])) {
            union(data[i][0], data[i][1]);
            weightSum += data[i][2];
        }
    }

    return weightSum;
}

public static void union(int a, int b) {
    int aP = find(a);
    int bP = find(b);

    if (aP != bP) {
        parents[aP] = bP;
    }
}

public static int find(int a) {
    if (a == parents[a]) {
        return a;
    }
    return parents[a] = find(parents[a]);
}

|  프림 구현

- 구현 순서

- 원리

입력받은 간선 데이터
int[][] graph = 
{{1, 3, 1}, {1, 2, 9}, {1, 6, 8}, 
{2, 4, 13}, {2, 5, 2}, {2, 6, 7}, 
{3, 4, 12}, 
{4, 7, 17}, {5, 6, 5}, {5, 7, 20}};

(1) 방문 배열 : 총 노드의 수(v)만큼 방문배열이 입력된다.

(2) 우선순위 큐

- 가중치의 크기를 기준으로 오름차순 자동 정렬

- 가장 작은 가중치의 노드를 꺼내, 방문 배열을 체크하고, 전체 가중치(weightSum)를 +하는 형태

  * 방문했던 노드는 다시 방문하지 않는다면, 결과적으로는 1-3-6-5-2-4-7 과 같이 노드가 연결될 것

- 타입 : Node (도착노드, 가중치)

- 구현

[1] 인접 리스트 및 방문 배열 초기화

static class Node{
    int to;
    int weight;
    
    Node(int to, int weight;){
    	this.to = to;
        this.weight = weight;
    }
}

public static int prim(int[][] data, int v, int e){
    // 인접리스트
    ArrayList<ArrayList<Node>> adjList = new ArrayList();
    for (int i = 0; i < v + 1; i++){
    	adjList.add(new ArrayList());
    }
    
    for (int i = 0; i < e; i++){
    	// 양방향으로 저장
    	adjList.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
        adjList.get(data[i][1]).add(new Node(data[i][0], data[i][2]));
    }
    
    // 방문 배열
    boolean[] visited = new boolean[v + 1];
}

[2] 우선 순위 큐를 통해 자동 정렬

public static int prim(int[][] data, int v, int e){
    // 생략
    
    // 우선순위 큐
    PriorityQueue<Node> pq = new PriorityQueue((x, y) -> x.weight - y.weight);
}

[3] 임의의 노드(ex. 1)를 선택한 후 낮은 가중치의 간선 연결 x 노드 수만큼 반복

public static int prim(int[][] data, int v, int e){
    // 생략
    
    // 우선순위 큐
    PriorityQueue<Node> pq = new PriorityQueue((x, y) -> x.weight - y.weight);
    pq.add(new Node(1, 0)); // 임의의 노드를 시작점으로 지정
    
    int cnt = 0; // 노드만큼만 반복
    while (!pq.isEmpty()){
    	Node cur = pq.poll();
        cnt++;
        
        // 방문 여부확인
        if (visited[cur.to]){
        	continue;
        }
        visited[cur.to] = true; // 방문 체크
        weightSum += cur.weight; // 전체 가중치 갱신
        
        // 반복 수 확인(마지막 뽑는 노드)
        if (cnt == v) {
        	break;
        }
        
        // 인접한 정점을 작은 가중치 순으로 offer
        for (int i = 0; adjList.get(cur.to).size(); i++){
        	Node adjNode = adjList.get(cur.to).get(i);
            
            if (visited[adjNode.to]) {
            	continue;
            }
            
            pq.offer(adjNode);
        }
        
    }
    
    return weightSum;
}

- 전체 코드

static class Node {
    int to;
    int weight;

    public Node(int to, int weight) {
        this.to = to;
        this.weight = weight;
    }
}

public static int prim(int[][] data, int v, int e) {
    int weightSum = 0;

    ArrayList<ArrayList<Node>> adjList = new ArrayList();
    for (int i = 0; i < v + 1; i++) {
        adjList.add(new ArrayList<>());
    }

    for (int i = 0; i < e; i++) {
        // 양방향으로 연결
        adjList.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
        adjList.get(data[i][1]).add(new Node(data[i][0], data[i][2]));
    }

    boolean[] visited = new boolean[v + 1];

    PriorityQueue<Node> pq = new PriorityQueue<>((x, y) -> x.weight - y.weight);
    pq.add(new Node(1, 0));

    int cnt = 0;
    while (!pq.isEmpty()) {
        Node cur = pq.poll();
        cnt++;

        if (visited[cur.to]) {
            continue;
        }
        visited[cur.to] = true;
        weightSum += cur.weight;

        if (cnt == v) {
            return weightSum;
        }

        // 인접한 정점을 작은 가중치 순으로 offer
        for (int i = 0; i < adjList.get(cur.to).size(); i++) {
            Node adjNode = adjList.get(cur.to).get(i);

            if (visited[adjNode.to]) {
                continue;
            }

            pq.offer(adjNode);
        }
    }

    return weightSum;
}

[ 참고 및 출처 ]

- 부트캠트 수업 내용 정리

- [Do it! 알고리즘 코딩 테스트 자바 편]

|  플로이드-워셜 알고리즘

- 모든 노드의 최단 경로를 구하는 알고리즘으로 전체 간선을 인접 행렬로 표현하고 dp를 통해 최단 경로를 구하는 방식

- 기능 : 모든 노드 간에 최단 경로 탐색

- 특징 : 음수 가중치 Ok, 동적 계획법의 원리를 사용

- 시간복잡도 : O(V3)

|  플로이드-워셜 구현하기

[1] 배열을 선언하고 초기화

- 각각의 노드를 Start지점으로 두고 모든 Start지점에 대한 최단 거리를 구할 예정

static int[][] distDP; // 행 : 출발점, 열 : 도착점
static final int INF = 100_000_000; // overflow방지 큰 값 지정

public static void floydWarshall(int V, int E, int[][] data, int start) {

    // 1. 배열을 선언하고 초기화
    distDP = new int[V + 1][V + 1];
    for (int i = 1; i < V + 1; i++) {
        for (int j = 1; j < V + 1; j++) {
            if (i != j) {
                distDP[i][j] = INF;
            }
        }
    }
        
}

[2] 노드의 각 인접 노드 경로 입력

- 먼저 dp에 인접 행렬를 입력하는 것

- 인접 행렬을 기준으로 각각의 경유지에 대한 최단 거리를 업데이트할 예정

// 2. 노드의 각 인접 노드 경로 입력
for (int i = 0; i < E; i++) {
    distDP[data[i][0]][data[i][1]] = data[i][2];
}

[3] 점화식으로 배열 업데이트

- 각각의 경유지에 관해서, 어떤 출발지~경유지 + 경유지~어떤 도착지가 최소일 경우를 구한다.

for 경유지 K에 관해
   for 출발지 S에 관해
    	for 도착지 E에 관해
          D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E]);

// 3. 점화식으로 배열 업데이트
// :  어떤 경유지를 거쳐 가는 것이 가장 빠른 가를 파악
for (int k = 1; k < V + 1; k++) { // 경유지
     for (int s = 1; s < V + 1; s++) { // 출발지
        for (int e = 1; e < V + 1; e++) { // 도착지
            // 경유지를 출발지 또는 도착지로 두는 거리가 입력된 바 없으면 무시
            if (distDP[s][k] != INF && distDP[k][e] != INF) {
                distDP[s][e] = Math.min(distDP[s][e], distDP[s][k] + distDP[k][e]);
            }
        }
    }
}

[4] 음수 사이클의 경우

- 음수사이클의 경우, 위 알고리즘에서 자기자신의 dp지점이 음수로 나타나게 된다.

** 최종 코드

static int[][] distDP; // 행 : 출발점, 열 : 도착점
static final int INF = 100_000_000; // overflow방지 큰 값 지정

public static void floydWarshall(int V, int E, int[][] data, int start) {

    // 1. 배열을 선언하고 초기화
    distDP = new int[V + 1][V + 1];
    for (int i = 1; i < V + 1; i++) {
        for (int j = 1; j < V + 1; j++) {
            if (i != j) {
                distDP[i][j] = INF;
            }
        }
    }

    // 2. 노드의 각 인접 노드 경로 입력
    for (int i = 0; i < E; i++) {
        distDP[data[i][0]][data[i][1]] = data[i][2];
    }

    // 3. 점화식으로 배열 업데이트
    // :  어떤 경유지를 거쳐 가는 것이 가장 빠른 가를 파악
    for (int k = 1; k < V + 1; k++) { // 경유지
         for (int s = 1; s < V + 1; s++) { // 출발지
            for (int e = 1; e < V + 1; e++) { // 도착지
                // 경유지를 출발지 또는 도착지로 두는 거리가 입력된 바 없으면 무시
                if (distDP[s][k] != INF && distDP[k][e] != INF) {
                    distDP[s][e] = Math.min(distDP[s][e], distDP[s][k] + distDP[k][e]);
                }
            }
        }
    }

    // 출력
    for (int i = 1; i < V + 1; i++) {
        for (int j = 1; j < V + 1; j++) {
            if (distDP[i][j] >= INF) {
                System.out.printf("%5s ", "INF");
            } else {
                System.out.printf("%5d ", distDP[i][j]);
            }
        }
        System.out.println();
    }

}

[ 참고 및 출처 ]

부트캠프

Do it 알고리즘 코딩 테스트

|  벨만-포드

- 가중치가 양수만 있을 때에 다익스트라를 사용했다면,

- 가중치에 음수가 있을 때엔 벨만-포드를 사용한다.

- 기능 : 특정 출발 노드에서 도착 노드까지의 최단 경로 탐색

- 특징 : 가중치 음수 OK,  음수 사이클 여부 판단

- 시간 복잡도 : O(VE)

|  벨만-포드 구현하기

- 지난번에 구현했던 다익스트라의 우선순위 큐 버전으로 쓰면 음수도 커버가 가능한데

- 벨만-포드를 사용하게 되면 음수 사이클 여부까지 커버할 수 있다.

- 구현의 순서

[1] 에지 배열(또는 리스트) & 최단 경로 dp 배열 초기화

- 이 부분은 다익스트라의 노드 클래스가 간선 클래스로 바뀐 것 밖에 없다.

- Edge라는 클래스안에 출발지점, 도착지점, 가중치를 넣어 배열에 저장한다.(또는 리스트에 저장)

- 최단 경로 dp 배열

class Edge{
    int from;
    int to;
    int weight;
    
    public Edge(int from, int to, int weight) {
        this.from = from;
        this.to = to;
        this.weight = weight;
    }
}

public void Bellmanford(int v, int e, int[][] data, int start){
    // 1. 간선 정보 및 최단 경로 배열 초기화
    // 1-1. 간선 정보를 배열로 저장
    Edge[] edge = new Edge[e];
    for (int i = 0; i < edge.length; i++) {
        edge[i] = new Edge(data[i][0], data[i][1], data[i][2]);
    }

    // 1-2. 최단 경로 배열
    int[] distDP = new int[v + 1];
    for (int i = 1; i < v + 1; i++) {
        distDP[i] = Integer.MAX_VALUE;
    }
    distDP[start] = 0;
}

[2] 모든 에지를 하나씩 확인하여 최단 경로 업데이트

* D는 dp, S는 출발노드, e는 도착노드
D[s] != ∞ 이며, D[e] > D[s] + w 일 때, D[e] = D[s] + w

- 음수 사이클이 없을 때 최대 에지 사용 횟수는 V - 1이다.

* 만약 노드의 개수가 5개이고, 음수사이클이 없다면 아래와 같이 4번 반복하여 최단거리를 확인한다.

// 2. 모든 간선을 확인해 정답 배열 업데이트 하기
for (int i = 1; i < v + 1; i++) { // 간선 횟수 + 1만큼 (음수사이클 확인)
    for (int j = 0; j < e; j++) { // 각 간선에 대하여
        Edge cur = edge[j]; 

        if (distDP[cur.from] == Integer.MAX_VALUE) { // 초기화되지x간선 무시(간선X)
            continue;
        }

        // 기존 거리 > 새로운 거리 : 현재 출발지 + 가중치  
        if (distDP[cur.to] > distDP[cur.from] + cur.weight) {
            distDP[cur.to] = distDP[cur.from] + cur.weight;
        }
    }
}

[3] 음수 사이클 여부 확인

- 만약에 음수 사이클이 없다면, 최대 에지 사용 횟수는 V 이상이다.

- 바깥 if문 안으로 들어오는 경우가 v번째이상인 경우는 음수사이클이 발생하므로 아래와 같이 작성해주면 완료된다.

if (distDP[cur.to] > distDP[cur.from] + cur.weight) {
    distDP[cur.to] = distDP[cur.from] + cur.weight;

    // 3. 음수 사이클 유무 확인하기
    if (i == v) {
        isMinusCycle = true;
    }
}

* 최종 코드 

public void bellmanFord(int v, int e, int[][] data, int start) {
    // 1. 간선 정보 및 최단 경로 배열 초기화
    // 1-1. 간선 정보를 배열로 저장
    Edge[] edge = new Edge[e];
    for (int i = 0; i < edge.length; i++) {
        edge[i] = new Edge(data[i][0], data[i][1], data[i][2]);
    }

    // 1-2. 최단 경로 배열
    int[] distDP = new int[v + 1];
    for (int i = 1; i < v + 1; i++) {
        distDP[i] = Integer.MAX_VALUE;
    }
    distDP[start] = 0;


    boolean isMinusCycle = false;
    // 2. 모든 간선을 확인해 정답 배열 업데이트 하기
    for (int i = 0; i < v + 1; i++) {
        for (int j = 0; j < e; j++) {
            Edge cur = edge[j];

            if (distDP[cur.from] == Integer.MAX_VALUE) {
                continue;
            }

            if (distDP[cur.to] > distDP[cur.from] + cur.weight) {
                distDP[cur.to] = distDP[cur.from] + cur.weight;

                // 3. 음수 사이클 유무 확인하기
                if (i == v) {
                    isMinusCycle = true;
                }
            }

        }
    }

    System.out.println("음수 사이클 발생 : " + isMinusCycle);
    for (int i = 1; i < v + 1; i++) {
        if (distDP[i] == Integer.MAX_VALUE) {
            System.out.print("INF" + " ");
        } else {
            System.out.print(distDP[i] + " ");
        }
    }
    System.out.println();

}

|  백준문제풀기

[ 출처 및 참조 ]

부트캠프 수업 내용 정리

 doit 알고리즘 코딩 테스트 책

|  다익스트라

- 가중치가 있는 그래프에서, 최단 경로를 구하는 알고리즘

- 핵심 : 그래프의 인접리스트와 DP를 이용

- 기능 : 출발 노드와 모든 노드 간의 최단 거리 탐색

- 특징 : 간선은 모두 양수

- 시간 복잡도 : O(ElogV) * E : 간선수, V : 정점수

|  다익스트라 구현

- 배열을 사용하는 것도 좋지만 배열 크기가 너무 클 경우를 대비해 인접 리스트를 사용

- (1),(2) 모두 기본적으로 동일하게 아래를 세팅

(1) 간선 정보 리스트 : 인접 리스트에 Node(연결된 노드, 가중치) 타입으로 저장

(2) 임시 거리 배열 : 출발지부터 노드 X까지의 현재 최소 거리를 업데이트할 배열

ㄴ start 위치는 자기 자신이므로 0으로 세팅한다.

class Node{
    int to;
    int weight;
    
    Node (int to, int weight){
    	this.to = to;
        this.weight = weight;
    }
}

// v : 간선수, data : 각 노드의 간선과 가중치 정보, start : 시작점
public void dijkstra(int v, int[][] data, int start){
    // (1) 간선 정보 업데이트
    ArrayList<ArrayList<Node>> adjList = new ArrayList();
    for (int i = 0; i < v + 1; i++){
    	adjList.add(new ArrayList());
    }
    
    for (int i = 0; i < data.length; i++){
    	adjList.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
    }  
}

// v : 간선수, data : 각 노드의 간선과 가중치 정보, start : 시작점
public void dijkstra(int v, int[][] data, int start){
	// (1) 간선 정보 업데이트
    ArrayList<ArrayList<Node>> adjList = new ArrayList();
    for (int i = 0; i < v + 1; i++){
    	adjList.add(new ArrayList());
    }
    
    for (int i = 0; i < data.length; i++){
    	adjList.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
    }  
    
    // (2) 현재까지 start부터 각 노드들까지 최소거리 dp 배열
    // : 초기값을 무한대(Integer.MAX_VALUE)로 설정한 후, 최소값을 갱신
    int distDP = new int[v + 1];
    for (int i = 1; i < v + 1; i++){
    	distDP = Integer.MAX_VALUE:
    }
    distDP[start] = 0; // start를 0으로 세팅
}

1. 방문 배열과 반복문 사용하기

(1) 먼저 방문 배열을 만들고, 첫번째 노드부터 끝 노드까지 현재 지점을 짚는다

// v : 간선수, data : 각 노드의 간선과 가중치 정보, start : 시작점
public void dijkstra(int v, int[][] data, int start){
    // (3) 방문 배열 + 반복문으로 다익스트라 구현
    
    // 방문배열
    boolean[] visited = new boolean[v + 1];
    
    // 반복문
    // start부터 각 노드들까지
    for (int i = 1; i < v + 1; i++){
        int minDistance = Integer.MAX_VALUE; // 최초 거리 : 무한대
        int curIdx = 0; // 최단 거리 노드
        
        // 1부터 V 중에 현재 노드
        for (int j = 1; j < v + 1; j++){
            if (!visited[j] && distDP[j] < minDistance){
            	minDistance = distDP[j];
                curIdx = j;
            }
        }
        
        visited[curIdx] = true;
        
        // 현재 노드에서 
        for (int j = 0; j < adjList.get(curIdx).size(); j++){
            // 연결된 노드들에 대하여
            Node adjNode = adjList.get(curIdx).get(j);
            
            if (distDP[adjNode.to] > distDP[curIdx] + adjNode.weight){
            	distDP[adjNode.to] = distDP[curIdx] + adjNode.weight;
            }
        }
    }
}

- 처음 Start부터 각 노드까지의 최선거리 DP는 모두 무한대(Integer.MAX_VALUE)로 2^32인 2147483647인 상태였다.

- 여기에 앞에서 기본 세팅해줄 때에 Start지점을 0으로 세팅했으므로 현재 상태는 아래와 같다.

- 위의 for문에서 아래 내용의 distDP[j] > minDistance는 따라서 가장 처음엔 Start값인 1이다.

// 1부터 V의 노드들 중에
for (int j = 1; j < v + 1; j++){
    // 현재 노드 짚기
    if (!visited[j] && distDP[j] < minDistance){
    	minDistance = distDP[j]; // minDistance = distDP[1];
        curIdx = j; // curIdx = 1;
    }
}

- 1 다음부터는 무한대 값인 녀석들을 처음에 curIdx로 짚어주고, 

(2) 현재노드부터 연결된 노드까지의 거리 중 최단 거리를 찾는다.

  (1) 현재까지  X노드까지 거리 : distDP[adjNode.to]

  (2) 새롭게 찾은 X노드까지 거리 : distDP[curIdx] + adjNode.weight 

  이 둘 중에 새롭게 찾은 (2) 가 더 작은 경우 갱신하라는 의미이다.

// 현재 노드에서 
for (int j = 0; j < adjList.get(curIdx).size(); j++){
    // 다시 파생되는 노드들에 대하여
    Node adjNode = adjList.get(curIdx).get(j);

    if (distDP[adjNode.to] > distDP[curIdx] + adjNode.weight){
        distDP[adjNode.to] = distDP[curIdx] + adjNode.weight;
    }
}

2. 우선순위 큐 사용하기

- 우선순위 큐는 원리는 비슷한데, 

- 공간이나 시간 복잡도 면에서 조금 더 개선된 코드이다.

- 하나씩 해보는 것이 필요한 코드..

boolean[] visited;

public void dijkstra(int v, int[][] data, int start){
    // (3) 방문 배열 초기화
    visited = new boolean[v + 1];

    // (4) 우선순위 큐를 통한 다익스트라 구현
    // -- 가중치 기준 오름차순으로 자동 정렬
    PriorityQueue<Node> pq = new PriorityQueue((x, y) -> x.weight - y.weight);
    pq.offer(new Node(start, 0)); // start지점을 0으로 갱신
    
    while (!pq.isEmpty()){
    	Node curNode = pq.poll(); // 현재 지점
        
        if (visited[curNode.to]) { // 방문 했던 곳은 X
            continue;
        }
        visited[curNode.to] = true; 
        
        for (int i = 0; i < adjList.get(curNode.to).size(); i++){ // 최단거리 갱신
            Node adjNode = adjList.get(curNode.to).get(i);
            
            if (!visited[curNode.to] && distDP[adjNode.to] > curNode.weight + adjNode.weight){
            	distDP[adjNode.to] = curNode.weight + adjNode.weight;
                pq.offer(new Node(adjNode.to, distDP[adjNode.to]);
            }
        } 
    }
}

|  백준 문제 풀이

[ 출처 및 참조 ]

부트캠프 수업 후 정리

Do it! 알고리즘 코딩 테스트

|  백트래킹

- 모든 가능한 경우의 수 중에서 유망하지 않은 쪽은 제외하고 최적해를 구하는 방법

- 주로 재귀를 사용해서 구현한다.

|  N-Queen 을 통한 백트래킹 이해

https://www.acmicpc.net/problem/9663

- N x N의 체스판에 N개의 퀸을 서로 공격할 수 없도록 배치한다고 할 때

- 메모리 공간 : 

(1) 각 행의 열을 짚어줄 배열

(2) 카운팅 변수

- Flow

(1) i번째 행의 각 열에 퀸을 배치한다.

(2) 유망여부 : 이전 행의 퀸 열의 상하좌우, 대각선에 해당되는가? 

- 2-1 ) YES : 다음 행으로 이동 

- 2-2 ) NO : 가지치기

(2) 모든 행을 다 돌은 경우, 방법의 수 카운팅

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;

public class Main {

    static int[] board; // 각 행의 퀸 열 위치
    static int cnt = 0; // 전체 카운트 수
    static int nQueen(int n, int r){
        // 탈출문
        if (r == n) {
            cnt++;
            //System.out.println(Arrays.toString(board));
            return cnt;
        }

        // 구현문
        // r번째 행에 대하여
        for (int i = 0; i < n; i++) {
            // 열 위치값 지정
            board[r] = i;

            // promising
            if (isPromising(r, i)){
                nQueen(n, r + 1);
            }
        }

        return cnt;
    }

    static boolean isPromising(int r, int c) {
        // 현재 행 전까지 겹치는 부분 확인
        for (int i = 0; i < r; i++) {
            int pre_r = i;
            int pre_c = board[i];

            if (pre_c == c || r - pre_r == Math.abs(c - pre_c)){
                return false;
            }
        }

        return true;
    }

    public static void main(String[] args) throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

        board = new int[N];

        System.out.println(nQueen(N, 0));
    }
}

|  그 외에 백트래킹을 사용하는 예시

(1) Permutation(순열)을 구하는 알고리즘 

import java.util.Arrays;

public class Practice {

    // 순열
    static int cnt = 0;
    static boolean[] visited;
    static int[] out;
    static int solution(int[] arr, int n, int r) {
        visited = new boolean[n];
        out = new int[r];

        return permutation(arr, n, r, 0);
    }

    static int permutation(int[] arr, int n, int r, int depth){
        if (depth == r){
            cnt++;
            System.out.println(Arrays.toString(out));
            return cnt;
        }

        for (int i = 0; i < n; i++) {
            if (visited[i] == false) {
                visited[i] = true;
                out[depth] = arr[i];
                permutation(arr, n, r, depth + 1);
                out[depth] = 0;
                visited[i] = false;
            }
        }

        return cnt;
    }

    public static void main(String[] args) {
        int[] arr = { 1, 2, 3 };
        int n = 3; // n개의 수 중에
        int r = 2; // r개의 수를 고르는 방법
        System.out.println(solution(arr, n, r));
    }
}

(2) N자리수에서 앞자리부터 일의 자리수, 십의 자리수... N의 자리수가 모두 소수인 수를 찾는 알고리즘

- 첫번째 자릿수는 무조건 2,3,5,7중 하나가 들어가야한다.

- 두번재 자릿수부터 0 ~ 9 중에 유망한 수를 구한다.

  > 유망하다 : 2나 5로 나누어떨어지지 않는 수

     > 백트래킹 : 현재까지 자릿수의 숫자(ex.233)가 소수인지 확인

  > 유망하지X : 가지치기 

public class Practice2 {

    static void solution(int n) {
        // 첫번째 자릿수는 무조건 2, 3, 5, 7 중 하나
        int[] primes = {2, 3, 5, 7};

        for (int i = 0; i < primes.length; i++) {
            getPrimes(primes[i], n,1);
        }
    }

    static void getPrimes(int prime, int n, int digitLen){
        
        if (digitLen >= n){
            System.out.print(prime + " ");
            return;
        }

        // 두번째 자릿수부터는 0 - 9중에
        for (int i = 0; i < 10; i++) {
            // 가지치기 : 2 또는 5로 나누어떨어지지 않는 수
            if (i % 2 != 0 && i % 5 != 0) {
                int primeCandidate = 10 * prime + i;

                // backtracking : 소수이면
                if (isPrime(primeCandidate)){
                    getPrimes(primeCandidate, n,digitLen + 1);
                }
            }
        }
    }
    
    static boolean isPrime(int n) {

        if (n < 2) {
            return false;
        }

        for (int i = 2; i <= Math.sqrt(n); i++) {
            if (n % i == 0) {
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        int n = 3;
        solution(n);
    }
}

|  백준 문제집

https://www.acmicpc.net/step/34

[ 출처 및 참조 ]

부트캠프 수업 후 정리한 내용입니다.