| 요약
| 핵심 단어 | 핵심 특성 | 언제 쓰면 좋을까 | |
| 트리 | 계층, Acyclic, 4가지의 순회 | 포화 이진 트리의 경우, 하위로 갈수록 노드의 갯수가 2^0, 2^1, 2^2..로 증가 |
계층 관계의 데이터를 다룰 때 |
| 그래프 | 네트워크, cyclic, DFS/BFS | 루트가 없고, 각 정점들간 단방향 또는 양방향의 관계를 가질 수 있음 |
연관 관계를 가진 데이터들에서 최적의 결과를 찾아야할 때 |
| 트리와 그래프의 차이
| 트리 | 그래프 | |
| 개요 | 그래프의 한 종류 | 정점(vertex, 노드)과 간선(edge)으로 이루어진 자료구조 |
| 그림 |  출처 : 위키백과 |
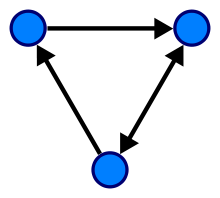 출처 : 위키백과 |
| 방향 | (단)방향 그래프 | 무(양)방향, (단)방향 그래프 |
| 사이클 | Acyclic | Cyclic |
| 모델 | 계층 모델 | 네트워크 모델 |
| 루트 | 최상위 노드 | 없음 |
| 상-하위 관계 | 인접한 상하위 노드 | 없음 |
| 간선의 갯수 | N개의 노드의 간선은 N-1개 | 그래프에 따라 다름 |
| 순회 | PreOrder, InOrder, PostOrder LevelOrder |
DFS BFS |
| 경로 | 두 노드 간 경로는 하나(단방향) | 두 노드 간 경로 여러 개 가능(양방향) |
| 종류 | 이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black트리), 이진 힙(최대힙, 최소힙) 등 |
- |
| 예시 | 폴더 구조(디렉토리, 서브 디렉토리), 조직도, 가계도 등 |
지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로 (교차점과 일방 통행길), 선수 과목 |
■ 트리 개요
| - 트리의 구조와 특징 - 이진 트리 - 이진 탐색 트리 - 균형 이진 탐색 트리 |
| 트리의 구조와 특징

[특징]
1. 모든 노드는 연결되어 있다.
2. 노드 간 이동 경로는 하나이다.(단방향)
3. 하나의 간선을 끊으면 2개의 sub-Tree로 나뉜다.
4. 이진트리에서, 노드가 N개인 트리의 간선 갯수는 N-1개이다.
5. 그래프와 달리 cycle이 존재하지 않는다(acyclic)| Basic | 노드(Node, 또는 정점) | data를 담고 있는 트리구조의 단위 |
| 간선(Edge) | 노드의 연결선 (= link, branch) | |
| 구분 | 루트(Root) | 꼭대기 노드 |
| 내부 노드(Internal) | 단말을 제외한 모든 노드 | |
| 단말(Leaf) | 자식이 없는 노드 | |
| 관계 | 부모(Parent) | 연결된 두 노드 중 상위 노드 |
| 자식(Child) | 연결된 두 노드 중 하위 노드 | |
| 형제(Sibling) | 같은 부모를 공유하는 노드 | |
| 깊이 | 깊이(Depth) | 루트에서 어떤 노드까지의 간선의 수 (ex. P에서 E까지 깊이 : 4) |
| 레벨(Level) | 트리의 특정 깊이를 가지는 노드 집합 (ex. level 1의 노드는 Q와 R) | |
| 높이(Height) | 트리에서 가장 큰 레벨 값 (ex. 위에 트리는 4) | |
| 노드 갯수 | 크기(Size) | 자신을 포함한 자식 노드의 갯수 |
| 간선 갯수 | 차수(Degree) | 각 노드가 가진 간선 갯수 (ex. L의 차수는 3) |
| 트리의 차수 | 트리의 최대 차수 (ex. 위 트리의 최대 차수는 L의 차수인 3) |
| 이진트리(BT, Binary Tree)
이진트리 : 최대 2개의 자식을 가질 수 있는 트리1. 이진 트리의 종류와 특징
| 포화 이진 트리(Perfect Binary Tree) | 모든 레벨에서 노드가 꽉 채워진 트리 |  |
| 완전 이진 트리(Complete Binary Tree) | 마지막 레벨을 제외하고 모든 레벨에서 노드가 꽉 채워진 트리 |
 |
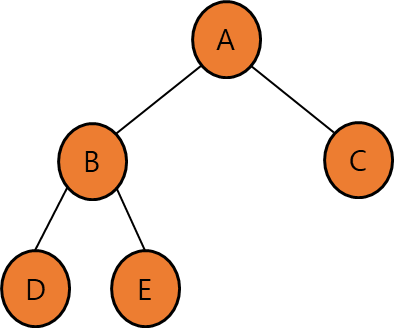
| 정 이진 트리(Full Binary Tree) | 모든 노드가 0 또는 2개의 자식을 가진 트리 (자식이 없거나 2개 모두 있거나) |
 |
| 편향 트리(Skewed Binary Tree, 사향 트리) | 한쪽으로 기울어진 트리 | 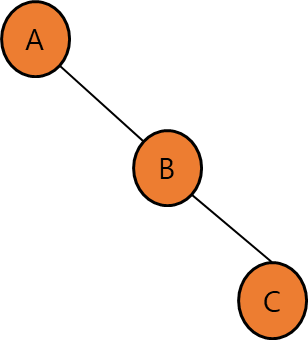 |
| 균형 이진 트리(Balanced Binary Tree) | 모든 노드의 좌우 서브 트리 높이가 1 이상 차이나지 않는 트리 (ex. 옆 그림에서 A의 좌측은 2개, 우측은 1개의 간선이 있어 차이가 1이 난다) |
 |
- 관련 수식
N = 2^(h+1) - 1
* N : 포화트리 노드의 갯수
* h : 높이h = logN
* N : 노드의 갯수
* h : 포화 또는 완전 트리 높이maxH = N
*maxH : 이진 트리의 최대 가능 높이
*N : 노드의 갯수
2. 이진 트리의 순회(Traversal)
| 전위 순회(PreOrder) | 현재 -> 왼쪽 -> 오른쪽 |
| 중위 순회(IntOrder) | 왼쪽 -> 현재 -> 오른쪽 |
| 후위 순회(PostOrder) | 왼쪽 -> 오른쪽 -> 현재 |
| 레벨 순회(LevelOrder) | 각 레벨에서 왼쪽 -> 오른쪽 |
[ 이진 트리를 구현할 때의 Tip ]
- 배열을 통해 이진 트리를 구현한다고 가정할 때 위치를 찾는 방법
(1) 좌측 노드 = 나의 노드 x 2 + 0 --> 배열idx에서는 나의 노드 x 2 + 1
(2) 우측 노드 = 나의 노드 x 2 + 1 --> 배열idx에서는 나의 노드 x 2 + 2
(3) 부모 노드 = 나의 노드 / 2
- 연결리스트를 통해 구성할 수도 있다.- 이진 트리 순회 구현 ▼ 더보기
1. 배열을 통한 이진트리 순회
// 배열을 통한 이진트리 구현
class BinaryTree{
char[] arr;
BinaryTree(char[] data){
this.arr = data;
}
public void preOrer(int idx){
System.out.print(arr[idx] + " ");
int left = 2 * idx + 1;
int right = 2 * idx + 2;
if (left < this.arr.length){
preOrder(left);
}
if (right < this.arr.length){
preOrder(right);
}
}
public void inOrder(int idx){
int left = 2 * idx + 1;
int right = 2 * idx + 2;
if (left < arr.length){
inOrder(left);
}
System.out.print(arr[idx] + " ");
if (right < arr.lenght){
inOrder(right);
}
}
public void postOrder(int idx){
int left = idx * 2 + 1;
int right = idx * 2 + 2;
if (left < arr.length) {
postOrder(left);
}
if (right < arr.length) {
postOrder(right);
}
System.out.print(arr[idx] + " ");
}
public void levelOrder(int idx){
for (int i = idx; i < arr.length; i++){
System.out.print(arr[i] + " ");
}
System.out.println("");
}
}
public class Main{
public static void main(String[] args){
BinaryTree bt = new BinaryTree(new char[]{'A','B','C','D','E','F','G'});
// A
// B C
// D E F G
}
}
2. 연결리스트를 통한 이진트리 순회
// 노드의 연결(연결리스트)을 통한 이진트리 구현
class Node{
char data;
Node left;
Node right;
Node(char data){
this.data = data;
}
}
class BinaryTree{
Node root;
BinaryTree(char[] datas){
Node nodes[] = new Node[datas.length];
// 각각의 노드를 생성
for (int i = 0; i < datas.length; i++){
nodes[i] = new Node(datas[i]);
}
// 트리 형태로 노드를 연결
root = nodes[0];
for (int i = 0; i < nodes.length; i++){
int left = i * 2 + 1;
int right = i * 2 + 2;
nodes[i].left = nodes[left];
nodes[i].right = nodes[right];
}
}
public void preOrder(Node node){
if (node == null) {
return;
}
preOrder(node.left);
System.out.print(node.data + " ");
preOrder(node.right);
}
public void inOrder(Node node){
if (node == null) {
return;
}
inOrder(node.left);
System.out.print(node.data + " ");
inOrder(node.right);
}
public void postOrder(Node node){
if (node == null){
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.print(node.data + " ");
}
public void levelOrder(Node node){
Queue<Node> queue = new LinkedList();
queue.add(node);
while (!queue.isEmpty()){
Node cur = queue.poll();
System.out.print(cur.data + " ");
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
}
}
public class Main{
public static void main(String[] args){
BinaryTree bt = new BinaryTree(new char[]{'A','B','C','D','E','F','G'});
// A
// B C
// D E F G
}
}
3. 가중치가 있는 포화이진트리의 루트~리프까지의 가중치 총합을 동일하게 만드는 최소합
BinaryTree{
int h; //높이
int sum; //가중치의합
int[] w; //가중치 배열
BinaryTree(int h, int[] w){
this.h = h;
this.w = new int[(int)(Math.pow(2, (h+1)))];
for (int i = 2; i < this.w.length; i++){
this.w[i] = w[i-2];
}
}
// 하위 좌우 중 더 큰 가중치에 맞춘 후 -> 상위 좌우 중 더 큰 가중치 합에 맞춘다.
public int dfs(int h, int idx){
if (h == this.h){
res += this.w[idx]; //리프 가중치 추가
return this.w[idx];
}
int leftW = dfs(h + 1, idx * 2 + 1); // 좌측 서브 트리의 가중치 합
int rightW = dfs(h + 1, idx * 2 + 2); // 우측 서브 트리의 가중치 합
res += this.w[idx] + Math.abs(leftW - rightW);
return this.w[idx] + Math.max(leftW, rightW); // 서브 트리에서 더 큰 가중치 합 반환
}
}
public class Main{
public static void solution(int h, int[] w) {
BinaryTree bt = new BinaryTree(h, w);
bt.dfs(0, 1);
System.out.println(bt.res);
}
public static void main(String[] args){
int h = 2;
int[] w = new int[]{1, 1, 2, 1, 3, 1};
solution(h, w);
}
}
| 이진 탐색 트리(BST, Binary Search Tree)
이진 탐색 트리 : 루트부터 시작하여 좌측에는 더 작은 키가, 우측에는 더 큰 키가 들어간 형태
* 모든 서브 트리 또한 이진 탐색 트리이며,
* 중복된 키는 허용하지 않는다.1. 이진 탐색 트리의 탐색 시간 복잡도
| 탐색 | 균형 상태 | O(logN) |
| 불균형 상태 | O(N) |
2. 이진 탐색 트리의 구현 - 탐색, 삽입과 삭제 (▼ 더보기)
| 탐색* | root에서부터 탐색. 찾으려는 key값이 현재 노드보다 작은 경우 좌측으로 이동, 큰 경우 우측으로 이동. 찾으려는 key값과 현재 노드의 키값이 같은 경우 탐색 완료 |
O(logN) |
| 삽입 | root에서부터 key값을 비교. 삽입하는 key값이 현재 노드보다 작은 경우 좌측으로 이동, 큰 경우 우측으로 이동. 이동한 현재 위치에 노드가 없는 경우(null), 그 위치에 노드를 추가 |
O(logN) |
| 삭제 | case1 삭제 노드가 리프인 경우 : 부모노드에서 리프방향을 null 처리 | O(logN) |
| case2 삭제 노드의 자식이 하나 있는 경우 : 부모노드에서 내 방향(ex.left)에 자식을 연결 | ||
| case2 삭제 노드의 자식이 둘인 경우 : (1) 부모노드에서 내 방향에 내 좌측자식에서 가장 큰 노드를 연결 (2) 부모노드에서 내 방향에 내 우측자식에서 가장 작은 노드를 연결 |
* 여기서의 탐색은 루트에서부터의 탐색으로, 이진 탐색 트리를 실제로 조회할 때는 4가지 순회 중 하나를 선택하는 것이 더 유리하다.(ex. preOrder/InOrder/....)
class Node{
int key;
Node left;
Node right;
Node(int key, Node left, Node right){
this.key = key;
this.left = left;
this.right = right;
}
}
class BinarySearchTree{
Node root;
BinatySearchTree(int key){
this.root = new Node(key, null, null);
}
// 삽입
public void add(int key){
if (root == null){
root = new Node(key, null, null);
} else {
Node cur = this.root;
Node pre = cur;
while (cur != null) {
pre = cur;
if (key < cur.key){
cur = cur.left;
if (cur == null){
pre.left = new Node(key, null, null);
break;
}
}
if (key > cur.key){
cur = cur.right;
if (cur == null) {
pre.right = new Node(key, null, null);
break;
}
}
}
}
}
// 삭제
public void remove(int key){
// 탐색 (해당 key값을 가진 노드 탐색)
Node cur = this.root;
Node parent = null;
while (cur != null){
if (cur.key == key){
break;
}
parent = cur;
if (key < cur.key) {
cur = cur.left;
} else {
cur = cur.right;
}
}
if (cur == null){ //없을 때
System.out.println("BinarySearchTree doesn't have key " + key);
}
// 세가지 case에 따라 삭제 진행
Node child = null;
Node leftRightMax = null;
Node ex;
// case 1 : 삭제 노드가 leaf 일 때
if (cur.left == null && cur.right == null){
if (cur == this.root){
this.root = null;
} else {
if (parent.left == cur){
parent.left = null;
} else {
parent.right = null;
}
}
}
// case 2 : 삭제 노드에 자식이 하나 있을 때
else if (cur.left != null && cur.right == null || cur.left == null && cur.right != null) {
// 자식 위치를 먼저 확인
if (cur.left != null) {
child = cur.left;
} else {
child = cur.right;
}
// 자식 노드를 현재 위치로 올린다.
if (parent == null){ // = cur 가 root
this.root = child;
} else {
if (parent.left == cur){
parent.left = child;
} else {
parent.right = child;
}
}
}
// case 3 : 삭제 노드에 자식이 둘 있을 때
else {
// 나의 좌측 노드 중 가장 큰 노드를 찾는다.
ex = cur;
leftRightMax = cur.left;
while (now.right != null){
ex = leftRightMax;
leftRightMax = leftRightMax.right;
}
// 나의 위치에 찾은 노드를 넣어준다.
ex.right = leftRightMax.left; // 먼저, 찾은 노드에 좌측노드가 있는 경우
leftRightMax.left = cur.left;
leftRightMax.right = cur.right;
if (parent == null){
this.root = leftRightMax;
} else {
if (parent.left == cur) {
parent.left = leftRightMax;
} else {
parent.right = leftRightMax;
}
}
}
}
}
| 균형 이진 트리 (추가 정리 예정)
(1) 이진 탐색 트리의 편향 발생
(2) 균형 이진 탐색 트리 종류
| AVL 트리 | red-black 트리 | |
| 공통점 | ||
| 차이점 |
■ 그래프 개요
| - 그래프의 구조와 특징 - 그래프의 탐색 - 그래프의 구현 |
| 그래프의 구조와 종류
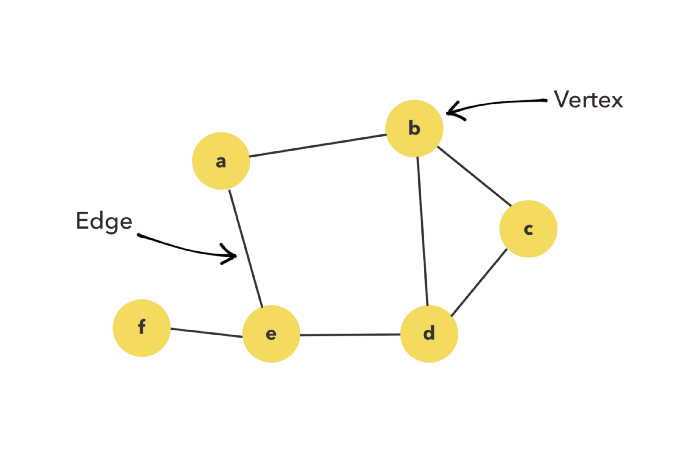
| Basic | 정점(Vertex, 노드) | 데이터를 담고 있는 노드 |
| 간선(Edge) | 연결선 = link, brank | |
| 관계 | 인접 정점(Adjacent vertex) | 간선 하나로 바로 연결된 정점 |
| 간선 갯수 |
정점의 차수(Degree) | 무방향 그래프에서 하나의 정점에 인접한 정점의 수 (ex. a노드의 차수는 2) * 무방향 그래프의 모든 정점 차수의 합 = 전체 간선의 수 x 2 |
| 진입 차수(In-degree) | 들어오는 간선의 수 | |
| 진출 차수(Out-degree) | 나가는 간선의 수 | |
| 경로 | 경로 길이(Path length) | 어떤 경로를 구성하는 데 사용된 간선의 수 |
| 단순 경로(Simple path) | 어떤 경로를 가기 위해 특정 정점을 반복해서 가지 않아도 되는 경우 | |
| 사이클 | 사이클(Cycle) | 단순 경로의 시작과 끝 정점이 동일한 경우 |


| 종류 | 내용 | 정점 A와 B의 간선 표현 / 비고 |
| 무방향 그래프(Undirected) | 간선에 방향이 없는 그래프 | (A, B) = (B, A) |
| 방향 그래프(Directed) | 간선에 방향이 있는 그래프 | <A, B> != <B, A> |
| 가중치 그래프(Weighted) | 간선에 값(이동 비용)이 있는 그래프 | - |
| 완전 그래프(Complete) | 모든 정점이 서로 연결된 그래프 | 정점이 N개일 때, 간선의 수 n(n-1)/2 |
| 그래프의 탐색
| DFS(깊이 우선 탐색) | = depth first search, Stack 또는 재귀를 사용하여 깊이 탐색 |
| BFS(너비 우선 탐색) | = breath first search, Queue를 사용하여 같은 레벨의 노드를 탐색 |
■ 그래프 탐색의 핵심
(1) 정점(Vertex)
(2) 간선(Edge, 곧 연결상태) : 어느 방향으로, 몇 개의 데이터가 연결되어 있는가
(3) 요구사항이 무엇인가?
ex.
- DFS
: 만약 root~leaf까지의 가중치를 구해야하거나,
: 바둑판과 같은 2차원 배열 or x축과 y축 좌표의 특정 위치에서 사방위로 움직일때
: 네트워크 방식으로 서로 복잡하게 연결된 정점들을 새로운 자료구조로 재구성할 경우
- BFS
: 어떤 정점 X에서 파생되는 여러개의 정점들이 있고, 각 하위 정점이 같은 규칙으로 파생될때
특정 타켓까지 구하기 위해서 얼만큼의 시도가 필요한가 (== level를 묻는 문제)
■ 인접 행렬 VS 인접리스트
- 간선 정보를 저장하는 자료구조로 인접 행렬과 인접 리스트를 주로 같이 설명하는데,
- 실제로 코딩테스트 문제를 풀다보면 HashSet를 쓰거나 HashMap을 통해서 간선 정보를 저장하기도 한다.
- DFS나 BFS를 써서 문제를 풀 때는 상황에 따라 가장 적절한 자료구조를 사용하는 것이 필요.
| 인접 행렬 | 인접 리스트 | ||
| 내용 | 2차원 배열로 인접 간선을 저장 | 연결리스트(LinkedList[])로 인접 간선을 저장 | |
| 장단점 | 간선 정보 확인/업데이트가 빠름 메모리 사용량이 높다(간선) |
정점의 추가/삭제가 빠르다. 메모리 사용량이 적다.(간선) 간선 정보 확인이 오래걸린다. |
|
| 언제 유리한가 | 정점의 갯수가 적고, 간선 갯수가 많을 때 | 정점의 갯수가 많고, 간선 갯수는 적을 때 | |
| 시간복잡도 |
특정 간선 탐색 | O(1) | O(degree(V)) *V: 차수 (특정 정점의 간선들) |
| 정점 차수 계산 | O(N) | O(degree(V)) | |
| 전체 정점 탐색 | O(N^2) *N : 정점 갯수 | O(E) *E : 간선 갯수 | |
| 공간복잡도 | N x N | N + E | |
| 그래프 문제
https://school.programmers.co.kr/learn/courses/30/parts/14393
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
https://school.programmers.co.kr/learn/courses/30/parts/12421
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
[ 참조 및 출처 ]
부트 캠프 수업을 들은 후 여러 참고 자료를 통해 내용을 정리하였습니다.
https://medium.com/@sarinyaswift/intro-to-the-graph-data-structure-a8277c6a2ad9
https://velog.io/@alstn3265/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC
'Computer Science > Data Structure' 카테고리의 다른 글
| [비선형 자료구조] 힙과 우선순위 큐 (0) | 2022.08.03 |
|---|---|
| 비선형 자료구조 총정리 (0) | 2022.08.03 |
| [선형자료구조] 해시테이블 (0) | 2022.07.22 |
| [선형자료구조] 스택, 큐, 데크 (0) | 2022.07.22 |
| [선형자료구조] 연결리스트 (0) | 2022.07.22 |