[비선형 자료구조] 힙과 우선순위 큐

simDev1234 2022. 8. 3. 22:20

| 들어가기 전에

- 왜 우선순위 큐는 비선형 구조일까?
: 큐는 선형구조로 1 : 1의 대응방식을 가진다. 앞에서 부터 데이터를 꺼내고, 뒤에서부터 데이터를 축척한다.
: 우선순위 큐는 이러한 큐에 우선순위 개념을 추가한 형태로, 우선순위를 따져 우선순위가 높은 데이터를 먼저 뽑는다.
: 우선순위 큐는 배열, 연결리스트, 힙으로 구현이 가능한데 이중에서 힙으로 구현을 하는 것이 가장 효율적이다.
: 따라서, 자바에서도 우선순위 큐는 힙으로 구현되었다. 힙은 완전 이진 트리 형태이며, 이는 1 : N 관계를 갖는 비선형구조이다.

- 자바에서는 우선순위 큐를 힙으로 구현한다. 왜?
: 위에서도 잠시 언급했던 것처럼, 힙으로 큐를 구현하는 것이 가장 효율적이기 때문에, 자바도 구현방식으로 힙을 쓴다.
- 배열의 경우, 중간 삽입 또는 삭제 시 O(N)의 시간이 소요되고,
- 연결리스트의 경우, 첫 위치에 삽입/삭제할 경우 O(1)이 걸리지만 그렇지 않다면 모든 구간을 돌아 O(N)이 소요된다.
- 힙의 경우, 루트에 최소값 또는 최대값을 두며 하위 트리로 파생되기 때문에 삽입/삭제 모두 logN이 걸린다.

자료구조	삽입	삭제
순서 없는 배열	O(1)	O(N)
순서 없는 연결리스트	O(1)	O(N)
정렬된 배열	O(N)	O(1)
정렬된 연결리스트	O(N)	O(1)
힙	O(logN)	O(logN)

: 이처럼, 힙을 사용하면 삽입/삭제의 시간 복잡도를 줄일 수 있기에 자바도 우선순위 큐를 힙으로 구현한다.
: 참고로, 자바의 PriorityQueue 객체는 Queue와 달리 인터페이스가 아니라 일반 클래스이다.

| 힙이란?

- 사전적으로, "무언가를 차곡차곡 쌓아올린 자료구조"라는 뜻이다.

- 완전 이진 트리 형태의 자료구조

** 완전 이진 트리란? 마지막 레벨을 제외하고 모든 레벨의 노드가 꽉 채워진 상태인 트리

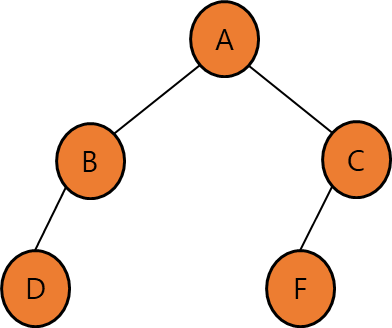
- 중복값을 허용하며, 반 정렬 상태(느슨한 정렬 상태)이다.

** 반 정렬 (또는 느슨한 정렬) 이란?
: 큰 값이 상위에 있고, 작은 값이 하위에 있을 뿐, 이진 탐색 트리처럼 좌우가 정렬되어 있지 않다.
** 중복값을 허용한다는 것은?
: 이진 탐색 트리와 달리, 힙은 중복값을 허용한다.

- 종류 : 최소힙, 최대힙

출처:https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

- 응용 분야 :

힙은 최대값과 최소값을 구해야할 때 가장 적절하다.
그렇기에 우선순위 큐를 구현하거나, 힙 정렬를 만드는 게 사용되며, 허프만 코드와 같은 알고리즘에 쓰인다.

| 힙의 구현

- 힙은 배열로 가장 잘 구현할 수 있다.

- 힙의 삽입은 아래와 같이 가장 끝에 데이터를 삽입하고 각 구간을 비교하여 교체하는 방식이며,

- 힙의 삭제는 최상단의 루트를 삭제하는 것으로, 가장 끝의 노드를 루트에 놓고 비교하여 교체하는 방식을 취한다.

삽입	(1) 트리의 가장 끝 위치에 데이터를 삽입 (2) 삽입한 위치의 부모노드와 비교하여 작으면 부모와 자리를 교체한다 (작지 않을 때까지 반복)
삭제	(1) 루트를 꺼내서 삭제한다. (2) 트리의 가장 끝 위치의 노드를 루트에 삽입 (3) 루트부터 시작해서 자식과 비교하여 자식보다 크면 교체한다. (크지 않을 때까지 반복)

[ 코드 - 더보기 ]

1. 최소힙 구현하기

import java.util.ArrayList;

class MinHeap{
    ArrayList<Integer> tree;

    public MinHeap(){
        this.tree = new ArrayList<Integer>();
        this.tree.add(0); // dummy data
    }

    // 삽입 : (1) 트리의 가장 뒤에 삽입 (2) 삽입 위치에서부터 부모와 비교
    public void add(int data){
        this.tree.add(data);

        int curIdx = this.tree.size() - 1; // 현재 위치
        int parentIdx = curIdx / 2; // 부모 위치
        while (curIdx > 1 && tree.get(parentIdx) > tree.get(curIdx)) {
            int tmp = tree.get(parentIdx);
            tree.set(parentIdx, tree.get(curIdx));
            tree.set(curIdx, tmp);
            curIdx = curIdx / 2;
        }
    }

    // 삭제 : (1) 루트를 삭제 (2) 루트에 가장 끝 노드를 삽입 (3) 루트에서부터 비교
    public int remove(){

        if (this.tree.size() == 1){
            System.out.println("this heap is empty!");
            return -1;
        }

        // (1)-(2)
        int min = this.tree.get(1);
        int last = this.tree.remove(this.tree.size() - 1);
        this.tree.set(1, last);

        // (3)
        int curIdx = 1;
        while(true){
            int leftIdx = curIdx * 2;
            int rightIdx = curIdx * 2 + 1;
            int childIdx = -1;

            if (rightIdx < this.tree.size()) { // 자식노드가 둘 다 있는 경우
                childIdx = tree.get(leftIdx) < tree.get(rightIdx) ? leftIdx : rightIdx;
            } else if (leftIdx < this.tree.size()) { // 자식노드가 하나인 경우
                childIdx = leftIdx;
            } else { // 자식이 하나도 없을 때
                break;
            }
            
            if (tree.get(curIdx) < tree.get(childIdx)){
                break;
            } else {
                int tmp = tree.get(curIdx);
                tree.set(curIdx, tree.get(childIdx));
                tree.set(childIdx, tmp);
                curIdx = childIdx;
            }
        }

        return min;
    }
}

2. 최대힙 구현하기

import java.util.ArrayList;

class MaxHeap{
    ArrayList<Integer> tree;

    public MaxHeap(){
        this.tree = new ArrayList<Integer>();
        this.tree.add(0); // dummy data
    }

    // 삽입 : (1) 트리의 가장 뒤에 삽입 (2) 삽입 위치에서부터 부모와 비교
    public void add(int data){
        this.tree.add(data);

        int curIdx = this.tree.size() - 1; // 현재 위치
        int parentIdx = curIdx / 2; // 부모 위치
        while (curIdx > 1 && tree.get(parentIdx) < tree.get(curIdx)) {
            int tmp = tree.get(parentIdx);
            tree.set(parentIdx, tree.get(curIdx));
            tree.set(curIdx, tmp);
            curIdx = curIdx / 2;
        }
    }

    // 삭제 : (1) 루트를 삭제 (2) 루트에 가장 끝 노드를 삽입 (3) 루트에서부터 비교
    public int remove(){

        if (this.tree.size() == 1){
            System.out.println("this heap is empty!");
            return -1;
        }

        // (1)-(2)
        int max = this.tree.get(1);
        int last = this.tree.remove(this.tree.size() - 1);
        this.tree.set(1, last);

        // (3)
        int curIdx = 1;
        while(true){
            int leftIdx = curIdx * 2;
            int rightIdx = curIdx * 2 + 1;
            int childIdx = -1;

            if (rightIdx < this.tree.size()) { // 자식노드가 둘 다 있는 경우
                childIdx = tree.get(leftIdx) > tree.get(rightIdx) ? leftIdx : rightIdx;
            } else if (leftIdx < this.tree.size()) { // 자식노드가 하나인 경우
                childIdx = leftIdx;
            } else { // 자식이 하나도 없을 때
                break;
            }

            if (tree.get(curIdx) > tree.get(childIdx)){
                break;
            } else {
                int tmp = tree.get(curIdx);
                tree.set(curIdx, tree.get(childIdx));
                tree.set(childIdx, tmp);
                curIdx = childIdx;
            }
        }

        return max;
    }
}

| 우선순위 큐란?

- 우선순위가 있는 큐이다.

- 모든 데이터가 우선순위가 있으며, Dequeue를 할 때에 우선순위가 높은 순으로 출력된다.

* 만약, 우선순위가 같은 경우에는 FIFO 순으로 출력된다.

■ 우선순위 큐를 어떻게 쓸 수 있을까?

- 우선순위 큐는 데이터를 삽입할때, 정해진 기준대로 오름차순/내림차순으로 데이터를 넣을 수 있고

- 최소값 또는 최대값부터 데이터를 뽑을 수 있다.

- 삽입/삭제 시간복잡도는 그럼 얼마나 될까? 앞에서 힙에서 언급했듯 logN이 걸린다.

- 이 점을 이용해서 K번째로 가장 큰 수를 뽑는다거나, 강도가 다른 돌을 부딪혀 남는 돌을 다시 넣거나,

중복된 수가 있는 수열에서 빈도수 기준으로 정렬하되 같은 빈도면 더 작은 수가 앞에 오게 정렬하는 등

순서에 따라 넣고 빼는 일이 잦거나 재정렬이 필요한 데이터들에서 사용할 수 있다.

■ Comparable 인터페이스

- 우선순위 큐를 사용할 때, 우선순위의 기준이 되는 객체에 Comparable인터페이스를 사용하면

오름차순 또는 내림차순으로 데이터를 enqueue/dequeue할 수 있다.
- Comparable인터페이스를 사용하는 방법은 크게 두가지이다.

[1] 객체에 Comparable를 구현하는 방법

class Student implements Comparable<Student>{
    String name;
    int score;

    public Student(String name, int score) {
        this.name = name;
        this.score = score;
    }

    @Override
    public int compareTo(Student o) {
        // this.Student(new)와 o(old) Student를 비교
        // 1 : 변경하지 않음, -1 : 변경
        return this.score >= o.score ? 1 : -1;
        // return this.score - o.score; -- 같은 말이다.
    }
}

[2] 람다식을 사용하여 비교 연산 메소드(compareTo)를 바로 구현하는 방법

import java.util.PriorityQueue;

class Student{
    String name;
    int score;

    public Student(String name, int score) {
        this.name = name;
        this.score = score;
    }
}

class test{
    public static void main(String[] args) {
        PriorityQueue<Student> pq = new PriorityQueue<>(
            (Student newSt, Student oldSt) ->  newSt.score - oldSt.score
        );

        for (int i = 0; i < 10; i++) {
            pq.add(new Student("Student"+(i+1), i * 10));
        }

        while(!pq.isEmpty()) {
            Student st = pq.poll();
            System.out.println(st.name + " : " + st.score);
        }
    }
}

[+] 문자열을 Comparable를 통해 사전순으로 offer/poll하는 방법

/* 생략 (위의 Student 객체 그대로 사용) */

class test{
    public static void main(String[] args) {
        PriorityQueue<Student> pq = new PriorityQueue<>(
            (Student newSt, Student oldSt) ->  newSt.name.compareTo(oldSt.name)
        );

        for (int i = 0; i < 10; i++) {
            char c = (char)('A' + (int)(Math.random()*32));
            pq.add(new Student((char)(c+i)+"_Student", i * 10));
        }

        /* 출력 생략 */
    }
}

| 힙과 우선순위 큐 문제

https://www.acmicpc.net/workbook/view/1819

문제집: 힙 쓰는 문제 (kcaladram)

www.acmicpc.net

https://www.acmicpc.net/step/13

우선순위 큐 단계

우선순위 큐를 응용하여 중앙값을 빠르게 찾는 문제

www.acmicpc.net

[ 참고 및 출처 ]

- 부트 캠프의 강의를 듣고 여러 자료들을 참조하여 정리한 내용입니다.

- https://namu.wiki/w/%ED%9E%99%20%ED%8A%B8%EB%A6%AC

- https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html